Edupanda » Teoria obwodów » Metoda Operatorowa
Metoda Operatorowa
Metoda operatorowa polega na zastąpieniu układu równań różniczkowych opisujacego dany obwód poprzez układ równań algebraicznych zmiennej s
Tok rozwiązania:
- Obliczenie warunków początkowych poprzez rozwiązanie układu w stanie przed przełączeniem
- Zastąpienie elementów przez ich wersje operatorowe
- Rozwiązanie nowopowstałego układu
- Obliczenie transformaty odwrotnej
Schematy operatorowe elementów RLC
Rezystor
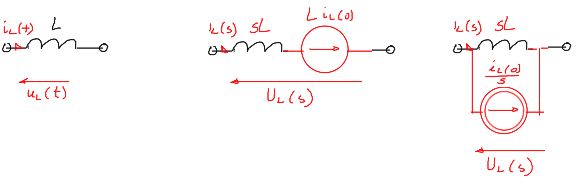
Cewka
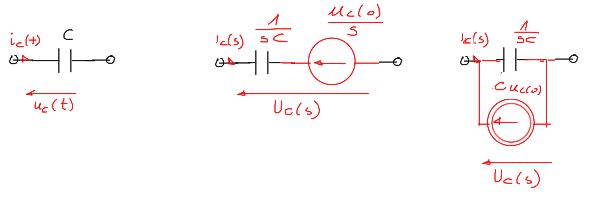
Kondensator
Dla przytłaczającej większości rozważanych obwodów transformate możemy zapisać w postaci: Pierwiastki licznika \(L(s)=0\) nazywamy zerami funkcji Pierwiastki mianownika \(M(s)=0\) nazywamy biegunami funkcji Aby obliczyć oryginał takiej transformaty możemy skorzystać ze wzorów zebranych poniżej: Korzystając z metody operatorowej wyznacz napięcie \(u_c(t)\) Dane: \(E_1=300 V, E_2=100 V, R_1=15 \Omega, R_2=25 \Omega, R_3=30 \Omega, C=50 mF=50 \cdot 10^{-3} F, L=2 H\) Rozwiązanie dla stanu przed przełączeniem (w celu wyznaczenia warunków brzegowych): Zamieniamy elementy na opis operatorowy, obliczamy korzystając z metody potencjałów węzłowych: Jak łatwo zauważyć \(u_C(s)=V\), więc pozostaje obliczyć transformatę odwrotną: Jak widać jest to wariant 2 z tabeli: Pozostaje obliczyć: \begin{aligned}
& u_R(t)=R i_R(t) \\
& \mathcal{L}\left[u_R(t)\right]=\mathcal{L}\left[R i_R(t)\right]\\
& U_R(s)=R I_R(s)\\
\end{aligned}
\begin{aligned}
& u_R(t)=R i_R(t) \\
& \mathcal{L}\left[u_R(t)\right]=\mathcal{L}\left[R i_R(t)\right]\\
& U_R(s)=R I_R(s)\\
\end{aligned}
 \begin{aligned}
& u_L(t)=L \frac{d i_L}{d t} \\
& \mathcal{L}\left[u_L(t)\right]=\mathcal{L}\left[L \frac{d i_L}{d t}\right]\\
& U_L(s)=s L I_L(s)-L i_L(0)\\
& I_L(s)=\frac{i_L(0)}{s}+\frac{U_L(s)}{L \cdot s}\\
\end{aligned}
\begin{aligned}
& u_L(t)=L \frac{d i_L}{d t} \\
& \mathcal{L}\left[u_L(t)\right]=\mathcal{L}\left[L \frac{d i_L}{d t}\right]\\
& U_L(s)=s L I_L(s)-L i_L(0)\\
& I_L(s)=\frac{i_L(0)}{s}+\frac{U_L(s)}{L \cdot s}\\
\end{aligned}
 \begin{aligned}
& i_C(t)=C \frac{d u_C(t)}{d t}\\
& \mathcal{L}\left[i_L(t)\right]=\mathcal{L}\left[C \frac{d u_C}{d t}\right]\\
& I_C(s)=s C U_C(s)-C u_C(0)\\
& U_C(s)=\frac{1}{s C} I(s)+\frac{1}{s C} u_C(0)\\
\end{aligned}
\begin{aligned}
& i_C(t)=C \frac{d u_C(t)}{d t}\\
& \mathcal{L}\left[i_L(t)\right]=\mathcal{L}\left[C \frac{d u_C}{d t}\right]\\
& I_C(s)=s C U_C(s)-C u_C(0)\\
& U_C(s)=\frac{1}{s C} I(s)+\frac{1}{s C} u_C(0)\\
\end{aligned}
Obliczanie transformaty odwrotnej
Lp.
Transformata
Pierwiastki
Oryginał
\(1\)
\(F(s)=\frac{L(s)}{M(s)} \)
pierwiastki mianownika rzeczywiste lub urojone
\(f(t)=\sum_{k=1}^n \frac{L\left(s_k\right)}{M^{\prime}\left(s_k\right)} \mathrm{e}^{S_k t}\)
\(2 \)
\(F(s)=\frac{L(s)}{s M(s)} \)
pierwiastki mianownika rzeczywiste i jeden s=0 (zerowy)
\(f(t)=\frac{L(0)}{M(0)}+\sum_{k=1}^m \frac{L\left(s_k\right)}{s_k M^{\prime}\left(s_k\right)} \mathrm{e}^{S_k t}\)
\(3\)
\(F(s)=\frac{L(s)}{M(s)}\)
pierwiastek mianownika jest podwójny (dwukrotny)
\(f(t)=\operatorname{res}_{s=s_k}\left[\frac{L(s)}{M(s)}\right]=\lim _{s \rightarrow s_k} \frac{d}{d s}\left[\frac{L(s)}{M(s)}\left(s-s_k\right)^2 \mathrm{e}^{s t}\right]\)
\(4 \)
\(F(s)=\frac{L(s)}{M(s)} \)
pierwiastki mianownika są zespolone sprzężone
\(f(t)=2 \operatorname{Re}\left[\frac{L\left(s_k\right)}{M^{\prime}\left(s_k\right)} \mathrm{e}^{S_k t}\right]\)
\(5 \)
\( F(s)=\frac{L(s)}{s M(s)} \)
pierwiastki mianownika są zespolone sprzężone i jeden s=0
\(f(t)=\frac{L(0)}{M(0)}+2 \operatorname{Re}\left[\frac{L\left(s_k\right)}{s_k M^{\prime}\left(s_k\right)} \mathrm{e}^{S_k t}\right]\)
Przykład 1
Treść
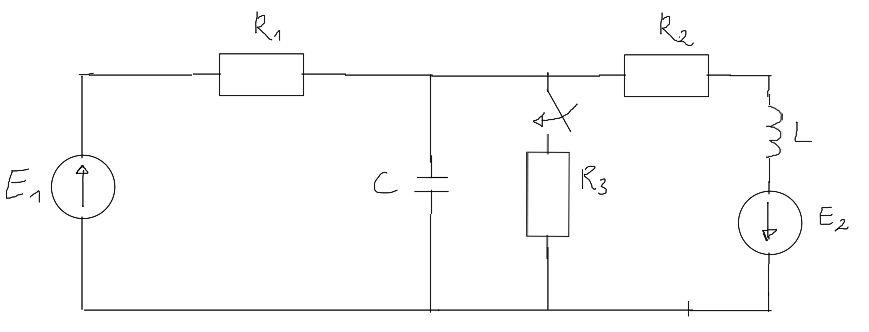
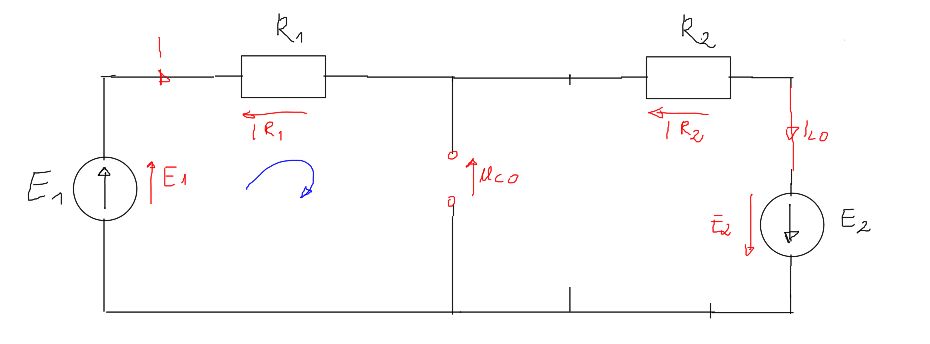
Rozwiązanie
 \[
\begin{aligned}
&I=\frac{E_1+E_2}{R_1+R_2}=10\\
&i_{L 0}=I=10\\
& E-I \cdot R_1-u_{C 0}=0 \\
& u_{C 0}=E_1-I \cdot R_1=150
\end{aligned}
\]
\[
\begin{aligned}
&I=\frac{E_1+E_2}{R_1+R_2}=10\\
&i_{L 0}=I=10\\
& E-I \cdot R_1-u_{C 0}=0 \\
& u_{C 0}=E_1-I \cdot R_1=150
\end{aligned}
\]
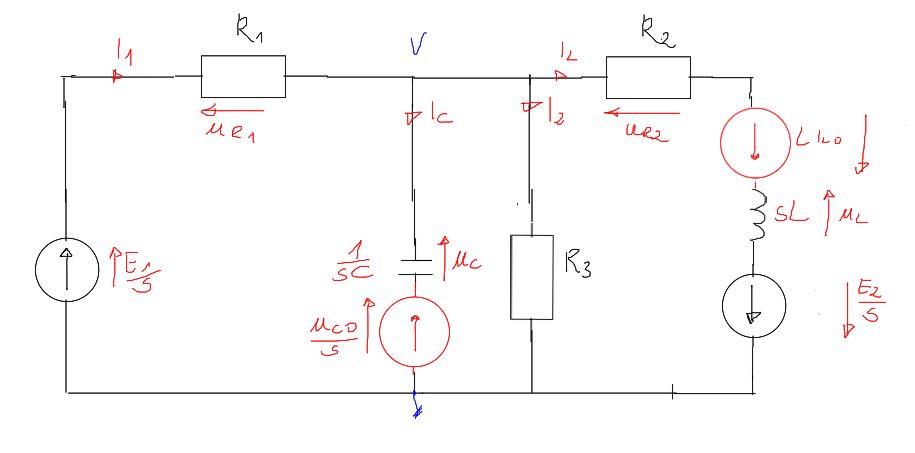 \begin{aligned}
& V \cdot\left(\frac{1}{R_1}+\frac{1}{\frac{1}{s \cdot C}}+\frac{1}{R_3}+\frac{1}{R_2+s \cdot L}\right)=\frac{\frac{E_1}{s}}{R_1}+\frac{\frac{u_{C 0}}{s}}{\frac{1}{s \cdot C}}-\frac{\frac{E_2}{s}+L \cdot i_{L 0}}{R_2+s \cdot L} \\
& V \cdot\left(\frac{s+2}{20}+\frac{1}{2 \cdot s+25}\right)=\frac{20 \cdot s+400}{s \cdot(2 \cdot s+25)}+\frac{15}{2} \\
& V=\frac{300 \cdot s^2+4150 \cdot s+8000}{s \cdot\left(2 \cdot s^2+29 \cdot s+70\right)}
\end{aligned}
\begin{aligned}
& V \cdot\left(\frac{1}{R_1}+\frac{1}{\frac{1}{s \cdot C}}+\frac{1}{R_3}+\frac{1}{R_2+s \cdot L}\right)=\frac{\frac{E_1}{s}}{R_1}+\frac{\frac{u_{C 0}}{s}}{\frac{1}{s \cdot C}}-\frac{\frac{E_2}{s}+L \cdot i_{L 0}}{R_2+s \cdot L} \\
& V \cdot\left(\frac{s+2}{20}+\frac{1}{2 \cdot s+25}\right)=\frac{20 \cdot s+400}{s \cdot(2 \cdot s+25)}+\frac{15}{2} \\
& V=\frac{300 \cdot s^2+4150 \cdot s+8000}{s \cdot\left(2 \cdot s^2+29 \cdot s+70\right)}
\end{aligned}

