Rozwiązanie
Figura ma jedną oś symetrii, więc na niej przyjmujemy jedną z osi układu. Drugą oś przyjmujemy dowolnie, na przykład po dolnej krawędzi jak poniżej.
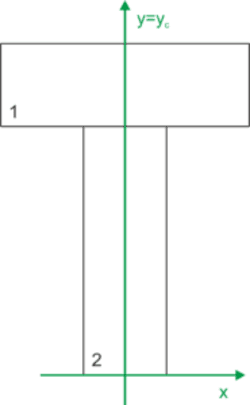
Szukamy pionowej współrzędnej środka ciężkości „yc”. Obliczamy ją jako iloraz statycznego momentu bezwładności i całkowitego pola przekroju. Dobrze sobie wypisać pomocniczo współrzędne „y-kowe” środków ciężkości poszczególnych figur prostych (y1 i y2) oraz ich pola (A1 i A2).
Obliczenie położenia środka ciężkości
\begin{aligned} &y_1=3,5a & A_1=3a^2\\ &y_2=1,5a & A_2=3a^2\\ &y_c=\frac{y_1A_1+y_2A_2}{A_1+A_2}=\frac{3,5a\cdot 3a^2+1,5a\cdot 3a^2}{3a^2+3a^2}=2,5a\\ \end{aligned}Zaznaczamy obliczony środek ciężkości na rysunku, a oś pozioma przeniesiona do środka ciężkości to oś główna centralna.
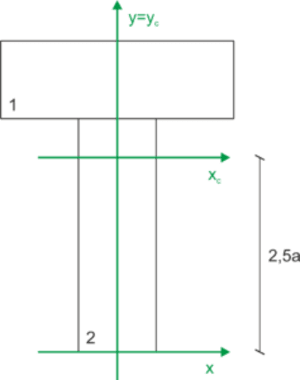
Obliczenie momentu bezwładności względem osi głównych centralnych
Do obliczenia momentu bezwładności względem osi poziomej musimy skorzystać z twierdzenia Steinera, dla osi pionowej nie jest to potrzebne.
\begin{aligned} &I_{XC}=I_{X1}+A_1(y_1-y_C)^2+I_{X2}+A_2(y_2-y_C)^2\\ &I_{XC}=\frac{3a\cdot a^3}{12}+3a^2(3,5a-2,5a)^2+\frac{a\cdot(3a)^3}{12}+3a^2(1,5a-2,5a)^2=8,5a^4\\ &I_{YC}=I_{Y1}+I_{Y2}\\ &I_{YC}=\frac{(3a)^3\cdot a}{12}+\frac{a^3\cdot 3a}{12}=2,5a^4\\ \end{aligned}