Żeby uzyskać dostęp do tego zadania musisz wykupić abonament ->
Sklep
Jeżeli masz już abonament a nadal widzisz ten komunikat upewnij się czy jesteś zalogowany
Przykład 16
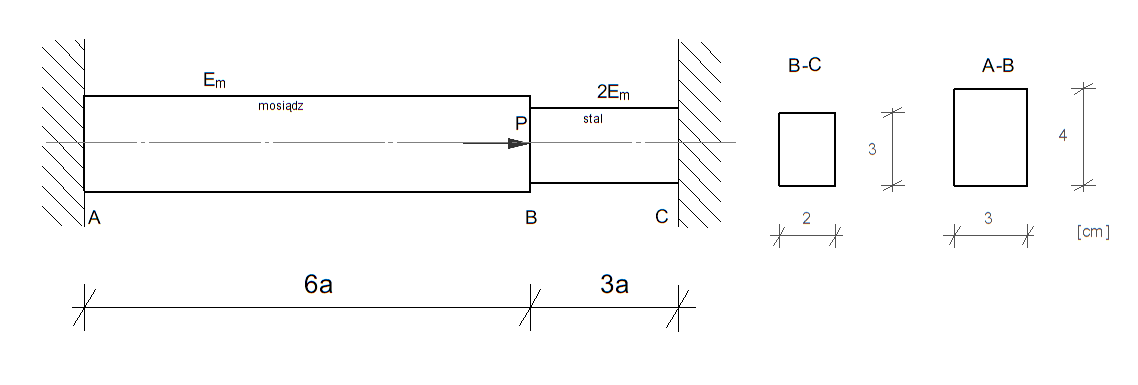
Dany jest pręt o zmiennym przekroju poddany działaniu osiowej siły \( P \). Na odcinku \( AB \) pręt wykonano z mosiądzu o \( E_m = 1 \cdot 10^5 \ \text{MPa} \) i \( R_{e1} = 200 \ \text{MPa} \), oraz na odcinku \( BC \) ze stali o \( E = 2E_m = 2 \cdot 10^5 \ \text{MPa} \) i \( R_{e2} = 250 \ \text{MPa} \). Wyznaczyć taką wartość obciążenia \( P = P_p \), przy którym największe naprężenie osiągnie wartość równą \( R_e \). Następnie, posługując się metodą stanów granicznych, wyznaczyć taką wartość \( P = P_r \), przy którym pręt osiągnie stan graniczny nośności. Wyznaczyć stosunek \( \frac{P_p}{P_r} \). Przyjąć \( a = 0{,}2 \ \text{m} \).