Ver introducción teórica al método de Maxwell-Mohr. También se proporciona más información y ejercicios sobre este tema.
Aprende más sobre la integración por método de Wereszczagina.

Solución del ejercicio:

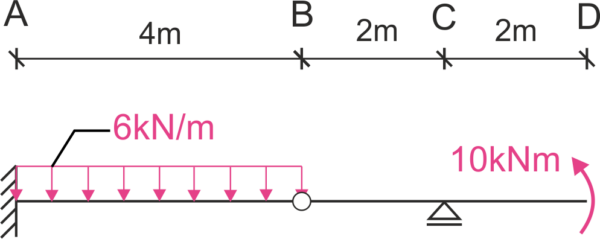
Descomponemos la viga articulada en vigas rectas, calculamos las reacciones y dibujamos los diagramas de fuerzas internas. Nota: las reacciones se pueden calcular sin descomponer en vigas rectas. No es necesario calcular el extremo para obtener el desplazamiento.

\begin{array}{cl} \mathbb{I} & \\ \sum M_{B}=0 & 10+2 V_{C}=0 \\ & V_{C}=-5 \mathrm{kN} \\ \sum Y=0 & V_{B}+V_{C}=0 \\ & V_{B}=5 \mathrm{kN} \end{array} \begin{aligned} \frac{29}{x}=\frac{29+5}{4}=>x=\frac{29 \cdot 4}{29+5}=\frac{58}{17} \approx 3,412 \end{aligned} \begin{array}{ll} \sum M_{A}=0 & -M_{A}-6 \cdot 4 \cdot 2-4 V_{B}=0 \\ & M_{A}=-68 \mathrm{kNm} \\ \sum Y=0 & V_{A}-6 \cdot 4-V_{B}=0 \\ & V_{A}=29 \mathrm{kN} \end{array} \begin{array}{cl} \mathbb{I} & \\ \sum M_{B}=0 & -1 \cdot 4+2 V_{C}=0 \\ & V_{C}=2 \mathrm{kN} \\ \sum Y=0 & V_{B}+V_{C}-1=0 \\ & V_{B}=-1 \mathrm{kN} \end{array} \begin{array}{ll} \text { II } & \\ \sum M_{A}=0 & -M_{A}-4 V_{B}=0 \\ & M_{A}=4 k N m \\ \sum Y=0 & V_{A}-V_{B}=0 \\ & V_{A}=1 k N \end{array}

Calculamos el desplazamiento teniendo en cuenta la influencia del momento flector (dominante) y la fuerza cortante. Si no tenemos datos numéricos, dejamos el resultado en la forma mostrada a continuación.

\begin{aligned} \Delta_{D}=& \int \frac{M_{P} M_{1}}{E I} d x+\kappa \int \frac{Q_{P} Q_{1}}{G A}=\\ =& \frac{1}{E I}\left[-\frac{1}{3} \cdot 4 \cdot 68 \cdot 4+\frac{1}{3} \cdot 4 \cdot 4 \cdot \frac{6 \cdot 4^{2}}{8}-\frac{1}{3} \cdot 2 \cdot 2 \cdot 10-\frac{1}{2} \cdot 2 \cdot 2 \cdot 10\right]+\\ &+\frac{\kappa}{G A}\left[-\frac{1}{2} \cdot 2 \cdot 29 \cdot 1+\frac{1}{3} \cdot 4 \cdot 5 \cdot 1+2 \cdot 1 \cdot 5\right]=\\ =&-332 \frac{1}{E I}-\frac{124}{3} \frac{\kappa}{G A} \end{aligned}