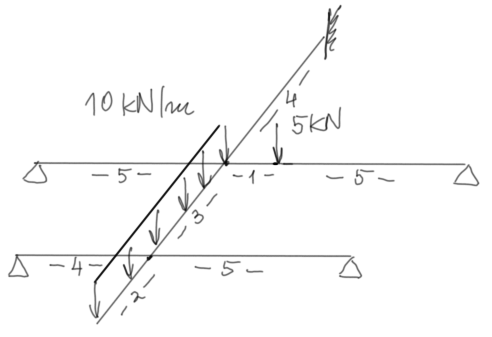
Rozwiązanie
Opisujemy punkty charakterystyczne
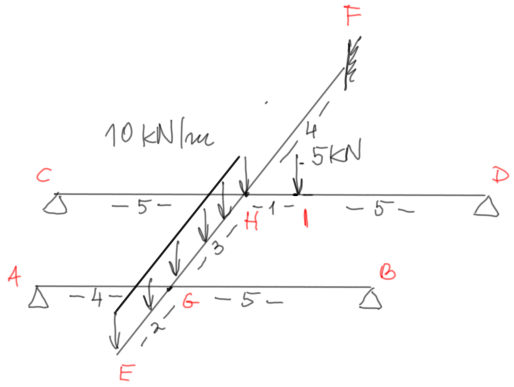 |
Stopień statycznej niewyznaczalności rusztu przegubowego można policzyć osobno dla każdej belki i do tego dodać liczbę połączeń między belkami - ta suma to SSN całego rusztu. \begin{array}{l} SSN=0^{AB}+0^{CD}+0^{EF}+2^{G,H}=2 \\ \end{array} Przyjmujemy układ podstawowy metody sił UPMS rozcinając połączenia między belkami w punkcie G i punkcie H, w miejsce siły działającej na łączeniu belek wstawiamy siły hiperstatyczne jednostkowe. UPMS rysuję już obracając wszystkie belki osobno do płaszczyzny kartki. |

Rysujemy teraz stany jednostkowe i stan P
Tym razem oprócz wykresu momentów w tych stanach narysowałem również wykresy sił tnących i skorzystam z nich rysując ostateczny wykres sił tnących.stan x1=1

stan x2=1

stan P

Współczynniki i wyrazy wolne równania kanonicznego
\begin{array}{l}
\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{20}{9} \cdot \frac{20}{9} \cdot 4+\frac{1}{3} \cdot \frac{20}{9} \cdot \frac{20}{9} \cdot 5+\frac{1}{3} \cdot 7 \cdot 7 \cdot 7\right)=\frac{3487}{27} \cdot \frac{1}{\mathrm{EI}} \\
\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{30}{11} \cdot \frac{30}{11} \cdot 5+\frac{1}{3} \cdot \frac{30}{11} \cdot \frac{30}{11} \cdot 6+\frac{1}{3} \cdot 4 \cdot 4 \cdot 4\right)=\frac{1604}{33} \cdot \frac{1}{\mathrm{EI}} \\
\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 4 \cdot 4 \cdot 7+\frac{1}{6} \cdot 4 \cdot 4 \cdot 3\right)=\frac{136}{3} \cdot \frac{1}{\mathrm{EI}} \quad \delta_{21}:=\delta_{12} \\
\delta_{1 \mathrm{p}}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{-1}{3} \cdot 3 \cdot 3 \cdot 125-\frac{1}{6} \cdot 3 \cdot 3 \cdot 20+\frac{1}{3} \cdot 3 \cdot 3 \cdot \frac{10 \cdot 3^2}{8}+\right]=-\frac{61655}{12} \cdot \frac{1}{\mathrm{EI}} \\
+\frac{-4}{6} \cdot(3 \cdot 125+7 \cdot 325+10 \cdot 450) \\
\delta_{2 \mathrm{p}}=\frac{1}{\mathrm{EI}} \cdot\left[\frac{1}{3} \cdot 5 \cdot \frac{30}{11} \cdot \frac{125}{11}+\frac{1}{6} \cdot\left(\frac{30}{11} \cdot \frac{125}{11}+\frac{25}{11} \cdot \frac{150}{11}+\frac{55}{11} \cdot \frac{275}{11}\right)+\right]=-\frac{127525}{66} \cdot \frac{1}{\mathrm{EI}} \\
+\frac{1}{3} \cdot \frac{25}{11} \cdot 5 \cdot \frac{150}{11}-\frac{1}{3} \cdot 4 \cdot 4 \cdot 325-\frac{1}{6} \cdot 4 \cdot 4 \cdot 125
\end{array}
Rozwiązanie równania kanonicznego metody sił
\begin{gathered}
\left\{\begin{array}{c}
\delta_{11} \cdot \mathrm{x}_1+\delta_{12} \cdot \mathrm{x}_2+\delta_{1 \mathrm{p}}=0 \\
\delta_{21} \cdot \mathrm{x}_1+\delta_{22} \cdot \mathrm{x}_2+\delta_{2 \mathrm{p}}=0
\end{array}\right. \\
\begin{cases}\mathrm{x}_1=38.401 & \mathrm{kN} \\
\mathrm{x}_2=3.936 & \mathrm{kN}\end{cases}
\end{gathered}
Rozpisanie ostatecznych momentów i sił tnących ze wzorów superpozycyjnych
\begin{array}{|l|c|}
\hline \mathrm{M}_{\mathrm{ost}}=\mathrm{M}_1 \cdot \mathrm{x}_1+\mathrm{M}_2 \cdot \mathrm{x}_2+\mathrm{M}_{\mathrm{P}} & \mathrm{Q}_{\mathrm{ost}}=\mathrm{Q}_1 \cdot \mathrm{x}_1+\mathrm{Q}_2 \cdot \mathrm{x}_2+\mathrm{Q}_{\mathrm{P}} \\
\hline \text { Belka } \mathrm{AB} & \\
\mathrm{M}_{\mathrm{G}}=\frac{20}{9} \cdot \mathrm{x}_1=85.336 & \mathrm{Q}_{\mathrm{AG}}=\frac{5}{9} \cdot \mathrm{x}_1=21.334 \\
& \mathrm{Q}_{\mathrm{GB}}=\frac{-4}{9} \cdot \mathrm{x}_1=-17.067 \\
\hline
\end{array}
\begin{array}{|l|l|}
\hline \mathrm{M}_{\mathrm{ost}}=\mathrm{M}_1 \cdot \mathrm{x}_1+\mathrm{M}_2 \cdot \mathrm{x}_2+\mathrm{M}_{\mathrm{P}} & \mathrm{Q}_{\mathrm{ost}}=\mathrm{Q}_1 \cdot \mathrm{x}_1+\mathrm{Q}_2 \cdot \mathrm{x}_2+\mathrm{Q}_{\mathrm{P}} \\
\hline \hline \text { Belka CD } & \mathrm{Q}_{\mathrm{C}}=\frac{6}{11} \cdot \mathrm{x}_2+\frac{25}{11}=4.42 \\
\mathrm{M}_{\mathrm{H}}=\frac{30}{11} \cdot \mathrm{x}_2+\frac{125}{11}=22.099 & \mathrm{Q}_{\mathrm{H} . \mathrm{L}}=\frac{6}{11} \cdot \mathrm{x}_2+\frac{25}{11}=4.42 \\
\mathrm{M}_{\mathrm{I}}=\frac{25}{11} \cdot \mathrm{x}_2+\frac{150}{11}=22.583 & \mathrm{Q}_{\mathrm{H} . \mathrm{P}}=\frac{-5}{11} \cdot \mathrm{x}_2+\frac{25}{11}=0.483 \\
& \mathrm{Q}_{\mathrm{I} . \mathrm{L}}=\frac{-5}{11} \cdot \mathrm{x}_2+\frac{25}{11}=0.483 \\
& \mathrm{Q}_{\mathrm{I} . \mathrm{P}}=\frac{-5}{11} \cdot \mathrm{x}_2-\frac{30}{11}=-4.517 \\
& \mathrm{Q}_{\mathrm{D}}=\frac{-5}{11} \cdot \mathrm{x}_2-\frac{30}{11}=-4.517 \\
\hline
\end{array}
\begin{array}{|l|l|}
\hline \mathrm{M}_{\mathrm{ost}}=\mathrm{M}_1 \cdot \mathrm{x}_1+\mathrm{M}_2 \cdot \mathrm{x}_2+\mathrm{M}_{\mathrm{P}} &{\mathrm{Q}_{\mathrm{ost}}=\mathrm{Q}_1 \cdot \mathrm{x}_1+\mathrm{Q}_2 \cdot \mathrm{x}_2+\mathrm{Q}_{\mathrm{P}}} \\
\hline \hline \text { Belka EF } & \\
\mathrm{M}_{\mathrm{G}}=-20 & \mathrm{Q}_{\mathrm{G} . \mathrm{L}}=-20 \\
\mathrm{M}_{\mathrm{H}}=3 \cdot \mathrm{x}_1-125=-9.796 & \mathrm{Q}_{\mathrm{G} . \mathrm{P}}=1 \cdot \mathrm{x}_1-20=18.401 \\
\mathrm{M}_{\mathrm{F}}=7 \cdot \mathrm{x}_1-325=-56.191 & \mathrm{Q}_{\mathrm{H} . \mathrm{L}}=1 \cdot \mathrm{x}_1-50=-11.599 \\
& \mathrm{Q}_{\mathrm{H} . \mathrm{P}}=1 \cdot \mathrm{x}_1+1 \cdot \mathrm{x}_2-50=-7.662 \\
& \mathrm{Q}_{\mathrm{F}}=1 \cdot \mathrm{x}_1+1 \cdot \mathrm{x}_2-50=-7.662 \\
\hline
\end{array}
Wykresy ostateczne

Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: