Metody numeryczne - Metoda różnic skończonych
Metoda polegająca na przybliżeniu pochodnej funkcji przez odpowiednie wzory różnicowe. W poniższych opracowaniu skupimy się na dwóch prostych zastosowaniach metody różnic skończonych:
- 1. Rozwiązywanie równań różniczkowych
- 2. Rozwiązywanie belek zginanych
Poszczególne pochodne zamieniamy na wzory różnicowe korzystając z poniższych wzorów
Centralne wzory różnicowe dla zagadnienia jednowymiarowego

\begin{aligned} &f^I=\frac{1}{2 h}\left(-v_{i-1}+v_{i+1}\right) \\ &f^{I I}=\frac{1}{h^2}\left(v_{i-1}-2 v_i+v_{i+1}\right) \\ &f^{I I I}=\frac{1}{2 h^3}\left(-v_{i-2}+2 v_{i-1}-2 v_{i+1}+v_{i+2}\right) \\ &f^{I V}=\frac{1}{h^4}\left(v_{i-2}-4 v_{i-1}+6 v_i-4 v_{i+1}+v_{i+2}\right) \end{aligned}
gdzie \( h \) - długość elementu.
Rozwiązywanie równań różniczkowych przy pomocy metody różnic skończonych
Ogólny tok postępowania w tym przypadku
- 1. Podział badanego przedziału na n elementów o długości h
- 2. Zastąpienie pochodnych w równaniu odpowiednimi wzorami różnicowymi
- 3. Rozpisanie równań różnicowych dla poszczególnych punktów
- 4. Uwzględnienie warunków brzegowych
- 5. Rozwiązanie układu równań w postaci macierzowej
Przykład 1
Treść
Rozwiązać problem brzegowy z danymi jak poniżej
\begin{aligned} &y^{\prime \prime}(x)=2 x \quad x \in[a . b] \\ &a=3 \quad b=7 \\ &y(a)=4 \\ &y^{\prime}(b)=2 \\ \end{aligned}Dzieląc przedział na \( n=4 \) elementy
Rozwiązanie
Długość pojedynczego elementu:
\begin{aligned} h=\frac{b-a}{n}=1 \end{aligned}Położenie poszczególnych węzłów
\begin{aligned} x_i=x_0+i\cdot h \end{aligned}Zamieniamy równanie \(y''(x)=2x\) korzystając ze wzorów różnicowych:
\begin{aligned} &\frac{1}{h^2}\left(i_{- 1}-2 \cdot i+i_{p 1}\right)=2 x \\ &i_{- 1}-2 \cdot i+i_{p 1}=h^2 \cdot 2 x \end{aligned}Dla każdego węzła \(i=1,2,3,4\) zapisujemy równanie różnicowe zgodnie z powyższym wzorem, pomocniczo zapisujemy wartośći x dla poszczególnych węzłów:
\begin{array}{lll} i=1 & i_0-2 \cdot i_1+i_2=h^2 \cdot 2 x_1 & x_1=x_0+h=4 \\ i=2 & i_1-2 \cdot i_2+i_3=h^2 \cdot 2 x_2 & x_2=x_0+2 h=5 \\ i=3 & i_2-2 \cdot i_3+i_4=h^2 \cdot 2 x_3 & x_3=x_0+3 h=6 \\ i=4 & i_3-2 \cdot i_4+i_5=h^2 \cdot 2 x_4 & x_4=x_0+4 h=7 \end{array}Uwzględniamy warunki brzegowe, również zamieniając je na wzory różnicowe
\begin{array}{lll} y(a)=4 & y_0=4 & \\ y^{\prime}(b)=2 & \frac{1}{2 h}\left(-i_3+i_5\right)=2 & -i_3+i_5=4 h \end{array}Zapisujemy powyższe równania w postaci macierzowej \(A\cdot y = B\)
\( \left[\begin{array}{cccccc} 1 & -2 & 1 & 0 & 0 & 0 \\ 0 & 1 & -2 & 1 & 0 & 0 \\ 0 & 0 & 1 & -2 & 1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{array}\right] \cdot\left[\begin{array}{l} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{array}\right]=\left[\begin{array}{c} h^2 \cdot 2 \cdot x_1 \\ h^2 \cdot 2 \cdot x_2 \\ h^2 \cdot 2 \cdot x_3 \\ h^2 \cdot 2 \cdot x_4 \\ 4 \\ 4 \cdot h \end{array}\right]=\left[\begin{array}{c} 8 \\ 10 \\ 12 \\ 14 \\ 4 \\ 4 \end{array}\right] \)I ostatecznie rozwiązanie (w tym przypadku uzyskane w programie Mathcad):
\( y=A^{-1} B=\left[\begin{array}{r} 4 \\ -31 \\ -58 \\ -75 \\ -80 \\ -71 \end{array}\right] \)W praktyce interesuje nas jedynie pierwsze 5 wyników, ponieważ ostatni znajduje się de facto poza przedziałem badanym \(i=5 -> x=8\)
Rozwiązanie analitycznego tego równania uzyskane klasycznymi metodami rozwiązywania równań różniczkowych:
\( y_{a n}(x)=\frac{x^3}{3}-47 x+136 \)
W tabeli zestawiono wartości wraz z błędami dla poszczególnych punktów
\( \begin{array}{|r|r|r|r|r|r|} \hline \mathrm{i} & x & y & y_a & \text { Bład bezwzgledny } & \text { Bład wzgledny } \\ \hline 0 & 3 & 4 & 4 & 0 & 0,00 \% \\ \hline 1 & 4 & -31 & -30,667 & 0,333 & 1,09 \% \\ \hline 2 & 5 & -58 & -57,333 & 0,667 & 1,16 \% \\ \hline 3 & 6 & -75 & -74 & 1 & 1,35 \% \\ \hline 4 & 7 & -80 & -78,667 & 1,333 & 1,69 \% \\ \hline \end{array} \)Ddybyśmy podzielili przedział na więcej elementów dokładność była by oczywiście większa, natomiast w takim przypadku konieczne byłoby użycie programów obliczeniowych typu Matlab
Rozwiązywanie belek zginanych przy pomocy metody różnic skończonych
Tok postępowania jest niemal identyczny jak w przypadku rozwiązywania równań różniczkowych, ponieważ wychodzimy od zależności pomiędzy przemieszczeniem i obciążeniem belki prostej:
\( \frac{d^4 v(x)}{d x^4}=\frac{q(x)}{E J} \)Który w zapisie różnicowym przyjmie postać:
\( \frac{d^4 v(x)}{d x^4}=\frac{p_y(x)}{E J} \Longrightarrow \frac{v_{i-2}-4 v_{i-1}+6 v_i-4 v_{i+1}+v_{i+2}}{h^4}=\frac{q_{i}}{E J} \)Lub w prostszym zapisie:
\( v_{i-2}-4 v_{i-1}+6 v_i-4 v_{i+1}+v_{i+2}=b_i, \quad b_i=h^4 \cdot \frac{q_{i}}{E J} \)
Problemy zaczynają się w momencie kiedy belka nie jest obciążona w sposób ciągły, ale np. poprzez przyłożenie do niej siły punktowej, obciążenia trapezowego itd., lub kiedy jej sztywność jest zmienna na długości belki. W takich przypadkach będziemy musieli sprowadzić obciążenie do obciążenia ciągłego.
Dodatkowo po obliczeniu wartości ugięcia belki w poszczególnych punktach skorzystamy ze znanych zależności które pozwolą nam obliczyć siłę tnącą oraz moment zginający:
Warunki brzegowe dla belek
Warunki brzegowe będą dla belki wynikały ze sposobu podparcia jak przedstawiono poniżej
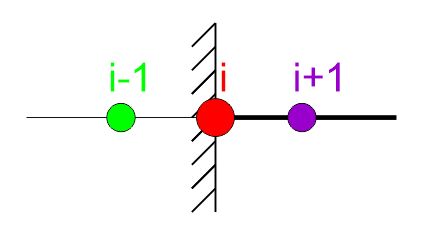
|
\begin{aligned} &v=0 \rightarrow v_{i}=0 \\ &\frac{d v}{d x}=0 \rightarrow \frac{-v_{i-1}+v_{i+1}}{2 h}=0 \end{aligned} |
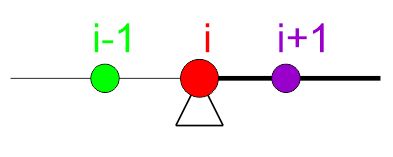
|
\begin{aligned} &v=0 \rightarrow v_{i}=0\\ &M=-E J \frac{d^2 v}{d x^2}=0 \rightarrow-E J \frac{v_{i-1}-2 v_i+v_{i+1}}{h^2}=0 \end{aligned} |
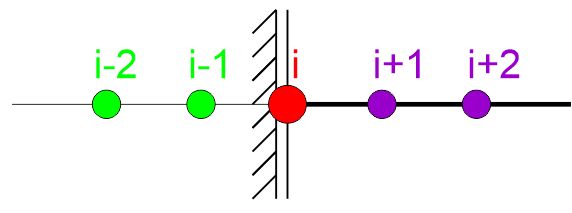
|
\begin{aligned} &\frac{d v}{d x}=0 \rightarrow \frac{-v_{i-1}+v_{i+1}}{2 h}=0 \\ &T=-E J \frac{d^3 v}{d x^3}=0 \rightarrow-E J \frac{-v_{i-2}+2 v_{i-1}-2 v_{i+1}+v_{i+2}}{2 h^3}=0 \end{aligned} |

|
\begin{aligned} &M=-E J \frac{d^2 v}{d x^2}=0 \rightarrow-E J \frac{-v_{i-1}-2 v_i+v_{i+1}}{h^2}=0 \\ &T=-E J \frac{d^3 v}{d x^3}=0 \rightarrow-E J \frac{-v_{i-2}+2 v_{i-1}-2 v_{i+1}+v_{i+2}}{2 h^3}=0 \end{aligned} |
Przykład 2
Treść
Rozwiązać podaną belkę korzystając z MRS, \(EI = 8000 kNm^2\)

Rozwiązanie
Zapisujemy równanie różnicowe dla punktów i=1,2,3,4
\( \begin{array}{ll} i=1 & 1 v_{-1}-4 v_0+6 v_1-4 v_2+1 v_3=b \\ i=2 & 1 v_0-4 v_1+6 v_2-4 v_3+1 v_4=b \\ i=3 & 1 v_1-4 v_2+6 v_3-4 v_4+1 v_5=b \\ i=4 & 1 v_2-4 v_3+6 v_4-4 v_5+1 v_6=b \end{array} \)gdzie \(b=\frac{h^4 \cdot q}{E I}\)
Następnie zapisujemy warunki brzegowe, w x=0, i=0 utwierdzenie pełne, w x=4, i=4 swobodny koniec
\begin{aligned} &v_0=0 \\ &-1 v_{-1}+1 v_1=0 \\ &1 v_3-2 v_4+1 v_5=0 \\ &-1 v_2+2 v_3-2 v_5+1 v_6=0 \end{aligned}Podobnie jak w poprzednim przykładzie zapisujemy całość w postaci macierzowej i rozwiązujemy przy pomocy programu obliczeniowego
\( \left[\begin{array}{cccccccc} 1 & -4 & 6 & -4 & 1 & 0 & 0 & 0 \\ 0 & 1 & -4 & 6 & -4 & 1 & 0 & 0 \\ 0 & 0 & 1 & -4 & 6 & -4 & 1 & 0 \\ 0 & 0 & 0 & 1 & -4 & 6 & -4 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & -2 & 1 & 0 \\ 0 & 0 & 0 & -1 & 2 & 0 & -2 & 1 \end{array}\right] \cdot\left[\begin{array}{c} v_{-1} \\ v_0 \\ v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \end{array}\right]=\left[\begin{array}{c} b \\ b \\ b \\ b \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right]=\left[\begin{array}{c} 1.25 \cdot 10^{-3} \\ 1.25 \cdot 10^{-3} \\ 1.25 \cdot 10^{-3} \\ 1.25 \cdot 10^{-3} \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right] \)\( \left[\begin{array}{l} v_{-1} \\ v_0 \\ v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \end{array}\right]=A^{-1} B=\left[\begin{array}{l} 5 \cdot 10^{-3} \\ 0 \\ 5 \cdot 10^{-3} \\ 1.562 \cdot 10^{-2} \\ 2.875 \cdot 10^{-2} \\ 4.25 \cdot 10^{-2} \\ 5.625 \cdot 10^{-2} \\ 7.062 \cdot 10^{-2} \end{array}\right] \)
Mając wartości ugięcia możemy obliczyć np. wartość momentu gnącego w utwierdzeniu
\( M_0=\frac{-E I}{h^2}\left(v_{-1}-2 \cdot v_0+v_1\right)=-80 kNM \)Akurat ta belka jest bardzo typowa, możemy więc z łatwością znaleźć analityczne rozwiązanie i porównać je z naszym, numerycznym
\( M_a=\frac{-1}{2} q \cdot L^2=-80kNm \)Jak widać rozwiązanie dla momentu zginającego jest identyczne, nieco bardziej interesująco ma się sprawa z ugięciem końca belki:
\begin{aligned} &v_a=\frac{q \cdot L^4}{8 E I}=4 \cdot 10^{-2} \\ &\frac{v_4-v_a}{v_a}=6.25 \% \end{aligned}Jak widać w tym przypadku błąd względny wynosi ponad 6%, podobnie jak poprzednio wyższe n sprawiłoby że ten błąd byłby mniejszy.
Bonus
W powyższym przykładzie pominęliśmy wartość siły tnącej w utwierdzeniu. Jak łatwo zauważyć stwarza ona pewien kłopot, ponieważ wzór:
\( T_0=-\frac{E I}{2 h^3}\left(-v_{-2}+2 \cdot v_{-1}-2 v_1+v_2\right) \)zawiera wartość przemieszczenia \(v_{-2}\) której nie obliczyliśmy. Jeżeli jednak w zadaniu mielibyśmy za zadanie obliczyć wartość siły tnącej musielibyśmy dodatkow zapisać wzór różnicowy dla i=0, co zilustrowano poniżej
\( \left[\begin{array}{ccccccccc} 1 & -4 & 6 & -4 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & -4 & 6 & -4 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & -4 & 6 & -4 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & -4 & 6 & -4 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & -4 & 6 & -4 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -2 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 2 & 0 & -2 & 1 \end{array}\right] \cdot\left[\begin{array}{l} v_{-2} \\ v_{-1} \\ v_0 \\ v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \end{array}\right]=\left[\begin{array}{l} b \\ b \\ b \\ b \\ b \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right] \)\( \left[\begin{array}{l} v_{-2} \\ v_{-1} \\ v_0 \\ v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \\ v_6 \end{array}\right]:=A^{-1} B=\left[\begin{array}{l} 2.562 \cdot 10^{-2} \\ 5 \cdot 10^{-3} \\ 0 \\ 5 \cdot 10^{-3} \\ 1.562 \cdot 10^{-2} \\ 2.875 \cdot 10^{-2} \\ 4.25 \cdot 10^{-2} \\ 5.625 \cdot 10^{-2} \\ 7.062 \cdot 10^{-2} \end{array}\right] \)
Oczywiście pozostałe wartości przemieszczenia nie zmieniły się, ale mając obliczone \(v_{-2}\) możemy zweryfikować wartość siły tnącej w utwierdzeniu:
\begin{aligned} &T_a=q \cdot L=40 kN \\ &T_0=-\frac{E I}{2 h^3}\left(-v_{-2}+2 \cdot v_{-1}-2 v_1+v_2\right)=40kN \end{aligned}Jak widać wynik jest idelanie zgodny z wartością analityczną

