Oblicz siłę krytyczną i sprawdź czy pręt ulegnie wyboczeniu. Dane: \( E=200 GPa, R_{e}=200 MPa, R_{h}=150 MPa \)

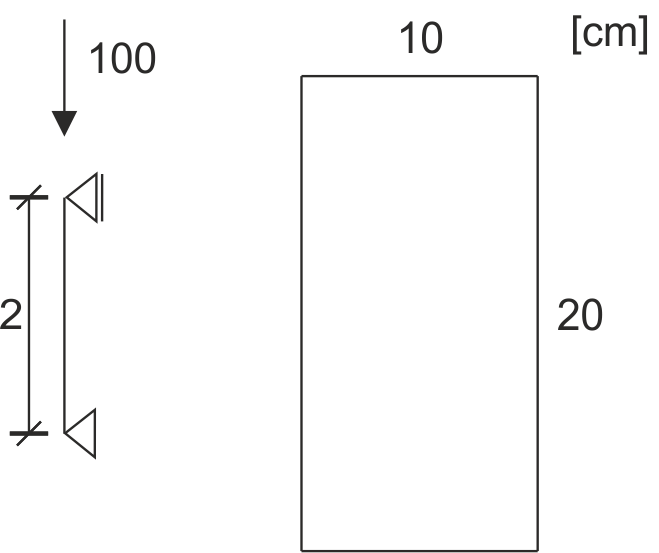
Oblicz siłę krytyczną i sprawdź czy pręt ulegnie wyboczeniu. Dane: \( E=200 GPa, R_{h}=150 MPa, R_{e}=200 MPa\)

Sprawdź czy pręt ulegnie wyboczeniu. Dane:\( l=5 m, E=205 GPa, R_{h}=150 MPa, a=240 MPa, b=0,56 MPa, P=800 kN\)

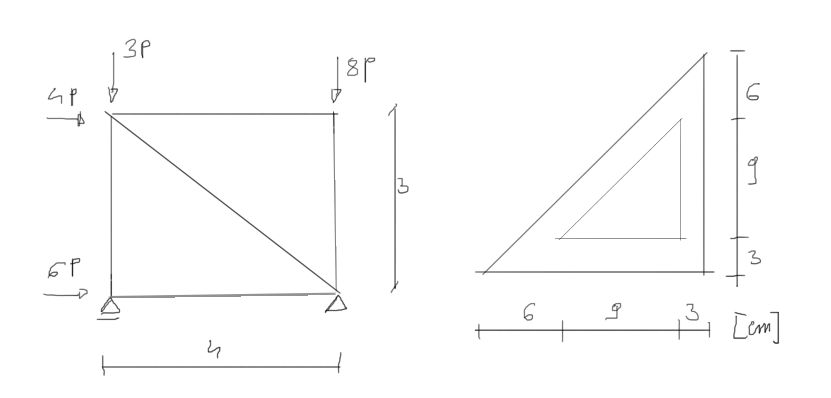
Jaką największą wartość może przyjąć siła P, aby żaden z prętów danej kratownicy nie uległ wyboczeniu? Przyjąc, że wszystkie pręty kratownicy mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami kratownicy, które nie mogą doznać przemieszczeń prostopadłych do płaszczyzny kratownicy.

Dany jest pręt osiowo ściskany o różnych warunkach podparacia w płaszczyznach XY i XZ. Wyznaczyć wmiary b i h tak, aby niebezpieczeństwo wyboczenia w obu płaszczyznach było jednakowe i smukłość pręta odpowiadała smukłości granicznej. Dane: \( E = 205 GPa, R_H = 200 MPa, E = 240 MPa, \)

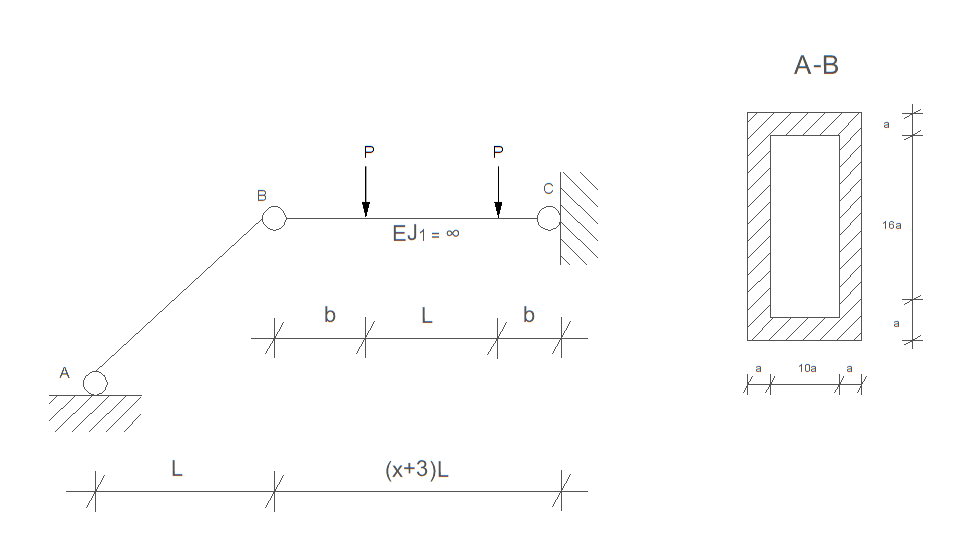
Dany jest podany obok układ składający się z dwóch prętów. Przyjmując \( L = 1\, \text{m} \), kąt \( \alpha = 60^\circ \) i \( P = 150\, \text{kN} \), wyznaczyć minimalną wartość \( a \), przy której pręt AB nie ulegnie wyboczeniu. Przyjąć przekrój pręta AB wg rysunku oraz założyć, że pręt AB ma swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami A i B stężonymi w kierunku prostopadłym do rysunku. Wyznaczyć ponadto wartość \( \lambda \), odpowiadającą smukłości granicznej pręta AB. (3 pkt.)

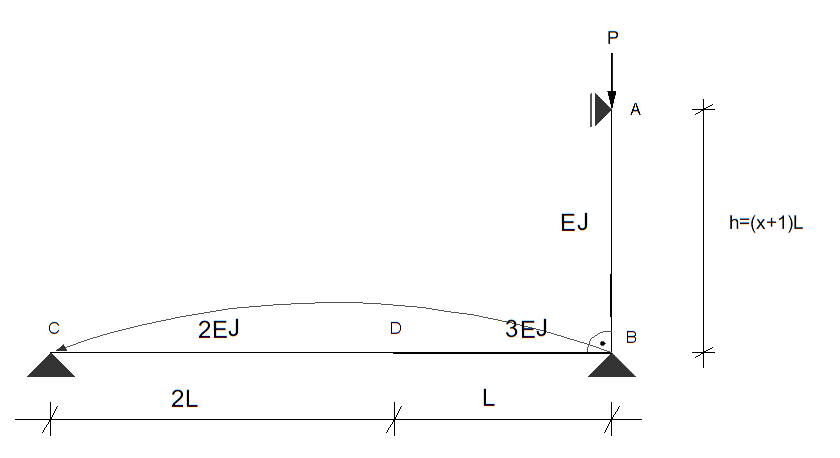
Korzystając z równania różniczkowego osi odkształconej (czwartego rzędu), wyprowadzić wzór na siłę krytyczną pręta ściskanego AB.

Uwaga: Rozwiązaniem zadania jest wzór na siłę krytyczną w zależności od parametrów \( E, J, L \) i ewentualnie jeszcze jednego dodatkowego parametru przyjętego do rozwiązania. Na ten dodatkowy parametr musi być zapisany warunek w postaci jednego równania.

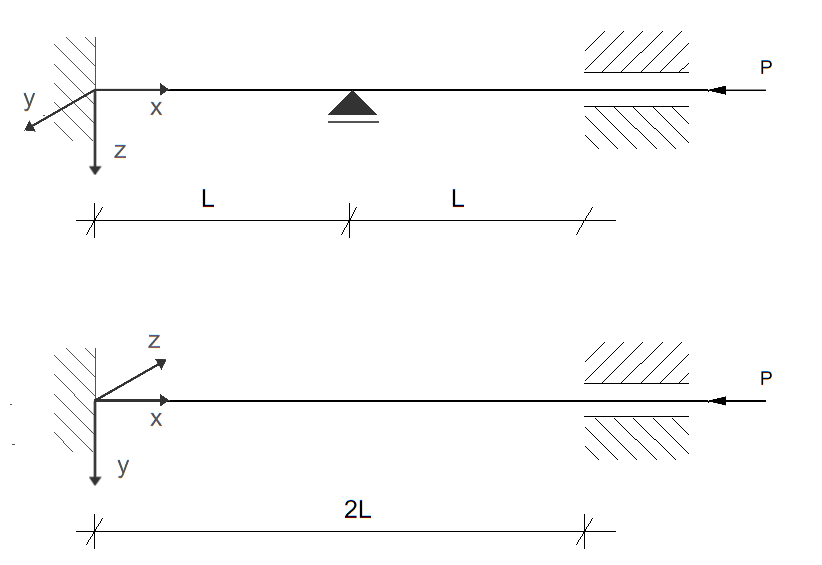
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach xy i xz, jak przedstawiono obok na rysunku. Przyjmując przekrój pręta w postaci dwóch kątowników jak podano na rysunku, wyznaczyć siłę krytyczną oraz naprężenie krytyczne rozważanego pręta. W obliczeniach przyjąć podane niżej wymiary i charakterystyki geometryczne pojedynczego kątownika:

\[ A = 17{,}1 \ \text{cm}^2, \quad J_{z_1} = J_{y_1} = 127 \ \text{cm}^4, \quad e = 2{,}58 \ \text{cm}, \quad L = 250 \ \text{cm}, \quad b = (4+x) \ \text{mm} \]

Ponadto przyjąć, że dzięki przewiązkom (tutaj nie narysowanym), dwa kątowniki w przekroju współpracują ze sobą przy przenoszeniu obciążenia.

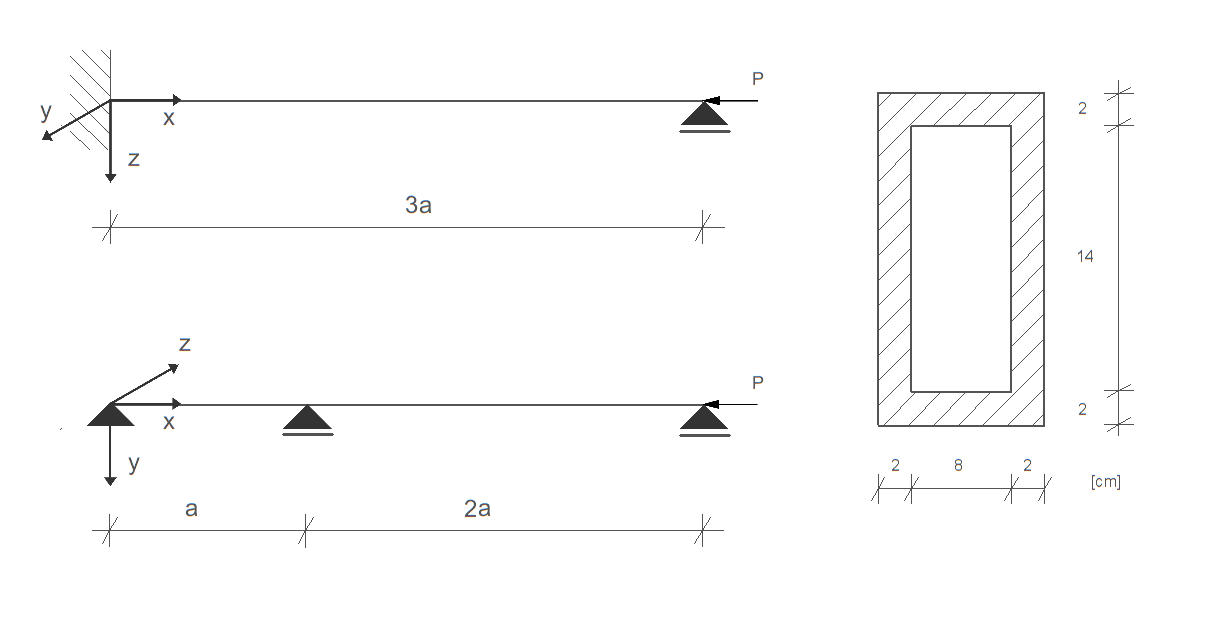
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach xy i xz jak przedstawiono obok na rysunku. Przyjmując \( E = 205 \, \text{GPa} \), \( R_H = 200 \, \text{MPa} \), \( R_{pl} = 240 \, \text{MPa} \) i \( a = 3 \, \text{m} \), wyznaczyć wartość siły krytycznej danego pręta.

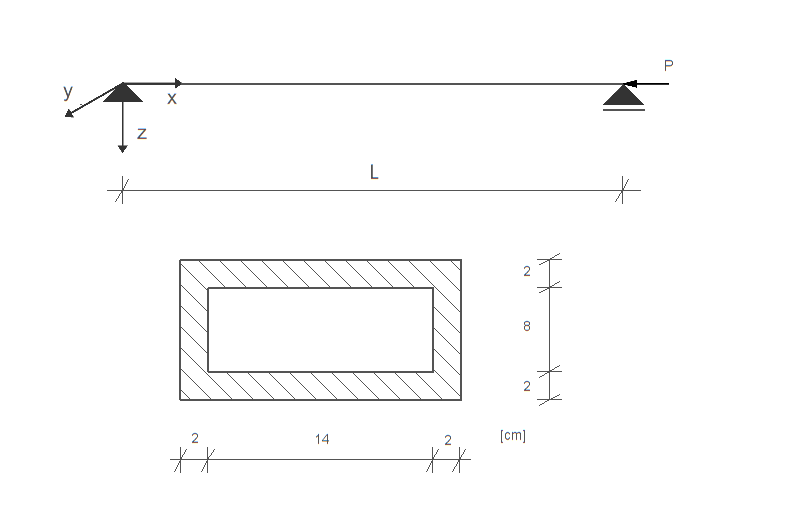
Dany jest pręt jednocześnie ściskany i zginany o schemacie podanym obok na rysunku. Korzystając z teorii I i II rzędu wyznaczyć wartości maksymalnego ugięcia i momentu zginającego w danym pręcie. Policz odpowiednie stosunki wyznaczonych wartości. W obliczeniach przyjąć \( E = 205 \, \text{GPa} \), \( l = 5 \, \text{m} \), \( M = 20 \, \text{kNm} \) oraz wartość siły \( P \) równą 30% wartości siły krytycznej, czyli \( P = 0{,}3 \cdot P_{kr} \). Ponadto obliczyć do jakiej maksymalnej wartości może wzrosnąć moment \( M \), aby strzałka ugięcia nie przekroczyła \( l / 200 \) oraz obliczyć wartość maksymalnego naprężenia normalnego związanego z tym momentem. Uwaga: Należy skorzystać z odpowiednich wyprowadzonych wzorów i przedstawionych w materiałach pomocniczych.

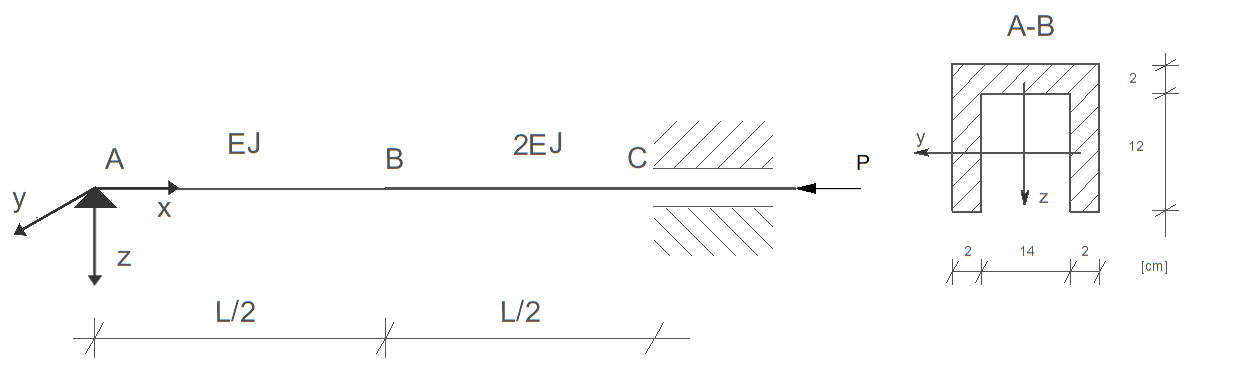
Dany jest pręt osiowo ściskany o przedstawiony obok na rysunku. Przyjmując \( E = 205 \ \text{GPa}, \quad R_H = 220 \ \text{MPa}, \quad R_{pl} = 260 \ \text{MPa}, \quad l = 4 \ \text{m} \), wyznaczyć wartość siły krytycznej danego pręta oraz — przyjmując krzywą wyboczeniową c — wyznaczyć nośność na ściskanie danego pręta wg wzoru empirycznego z PN-EN-1991-1-1:2006.

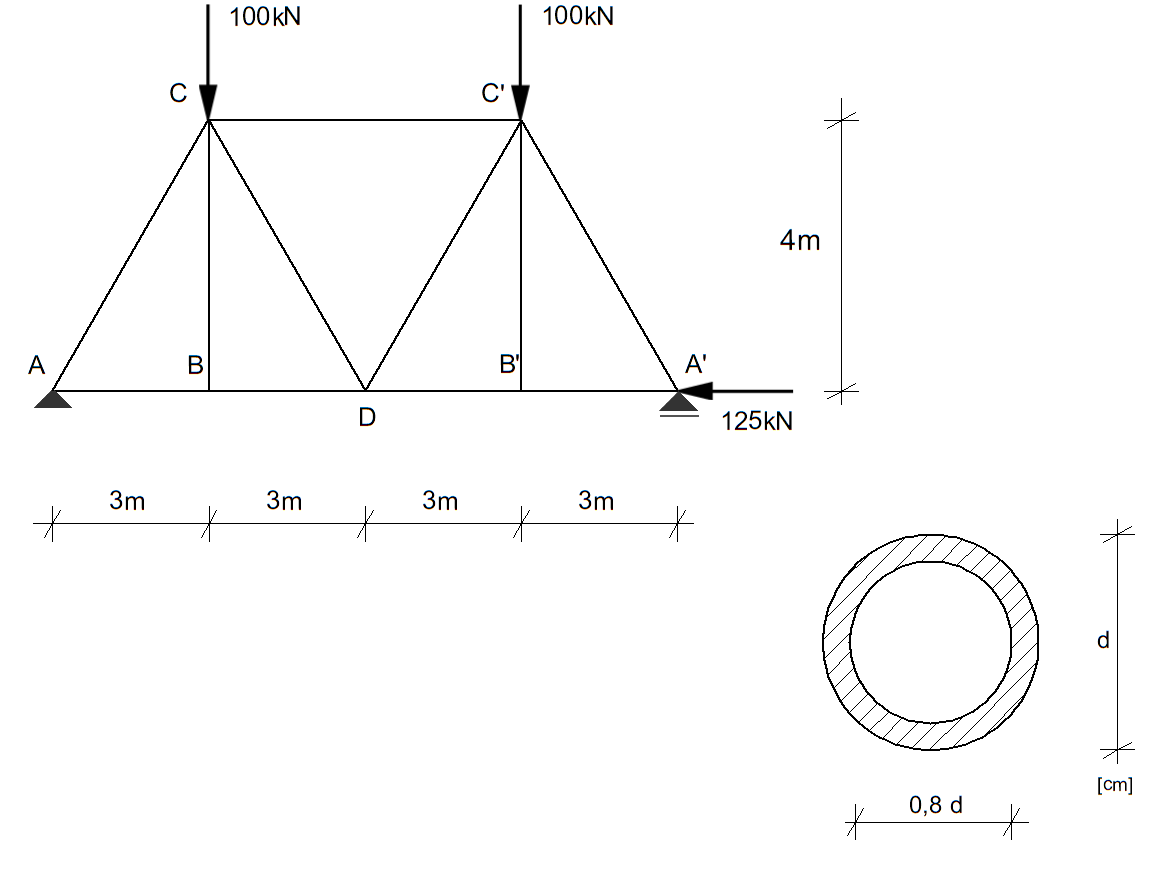
Dana jest symetryczna kratownica wykonana z prętów o przekroju pierścieniowym pokazanym na rysunku. Średnice poszczególnych prętów wynoszą: pręt AB i BD: \( d = d_1 \), AC: \( d = d_2 \), CC': \( d = d_3 \), CD: \( d = d_4 \), i BC: \( d = d_5 \). Pręty po stronie prawej mają średnice odpowiadające wynikające z warunku symetrii.

Wyznaczyć minimalne potrzebne średnice \( d \) wszystkich prętów ściskanych, aby żaden z nich nie uległ wyboczeniu i aby niebezpieczeństwo ich wyboczenia było jednakowe.

Przyjąć, że wszystkie pręty kratownicy mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami kratownicy, które nie mogą wyjść z jej płaszczyzny.

W obliczeniach przyjąć \( E = 72\,\text{GPa} \), \( R_H = 200\,\text{MPa} \), \( R_{pl} = 240\,\text{MPa} \).

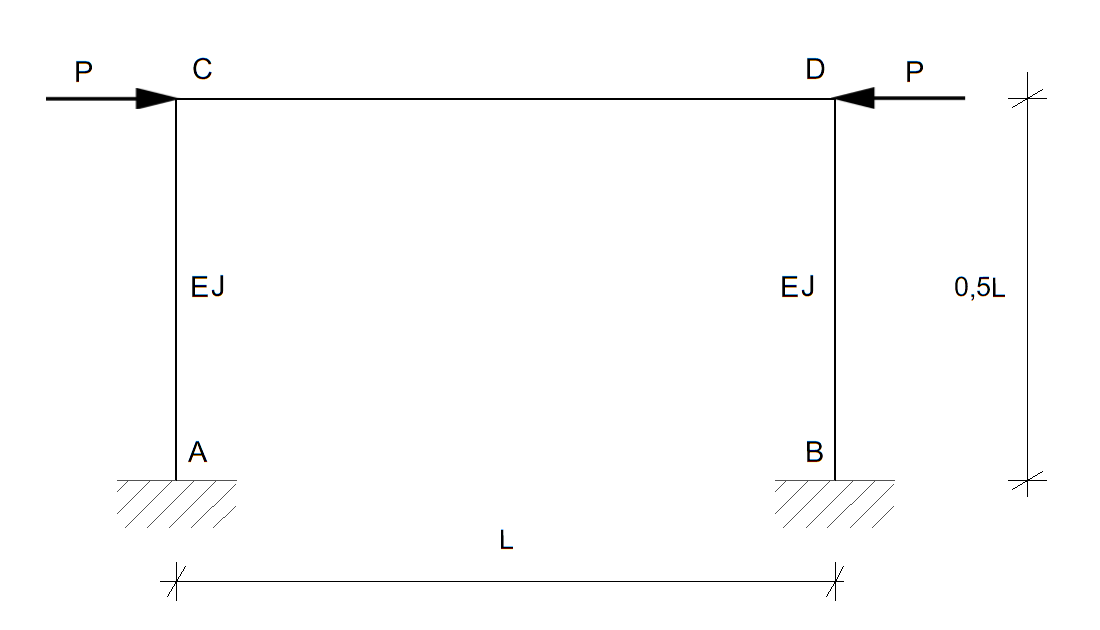
Korzystając z równania różniczkowego (czwartego rzędu) osi odkształconej pręta ściskanego wyprowadzić wzór na siłę krytyczną oraz wartość współczynnika wyboczeniowego pręta CD. Przyjąć symetryczną postać wyboczenia. W obliczeniach przyjąć nieskończoną sztywność na rozciąganie i ściskanie wszystkich prętów. Uwaga: Rozwiązaniem zadania jest wzór na siłę krytyczną w funkcji parametrów \( E \), \( J \), \( l \) i podana wartość współczynnika \( \mu \).

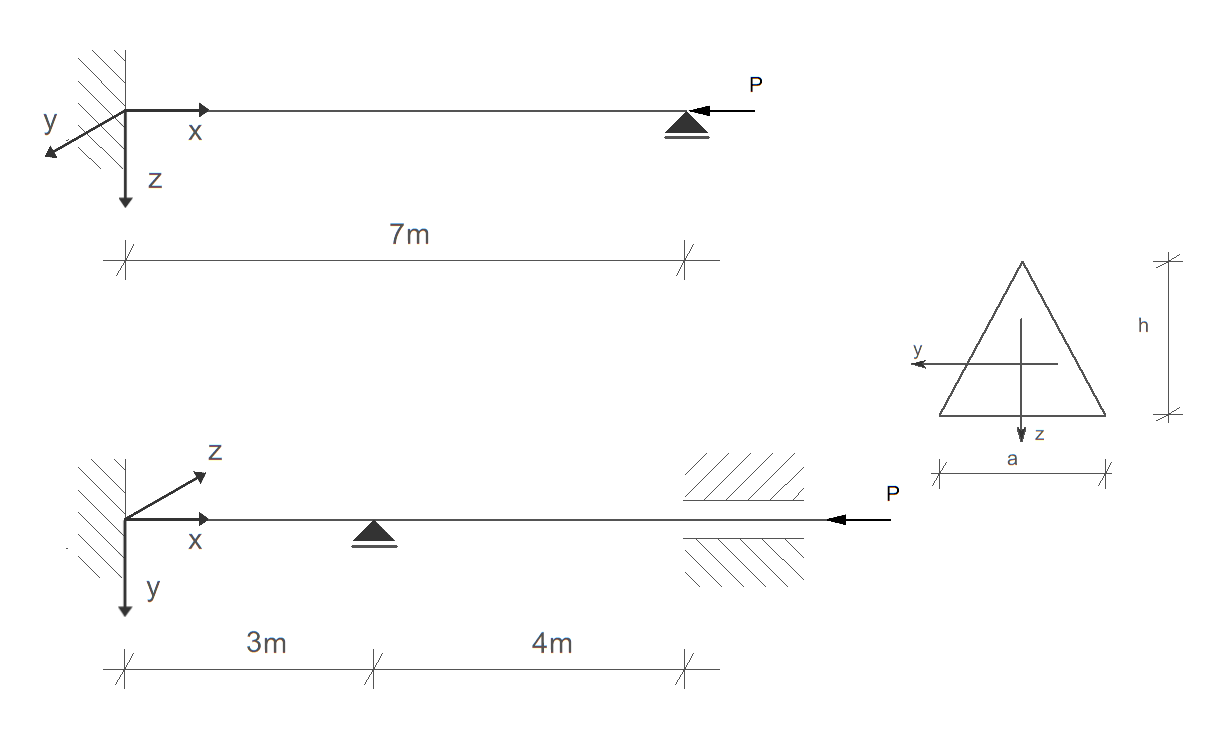
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach XY i XZ. Wyznaczyć wymiary a i h tak, aby niebezpieczeństwo wyboczenia w obu płaszczyznach było jednakowe i smukłość pręta odpowiadała smukłości granicznej. Przyjąć dane: \( E = 75 \, \text{GPa}, \quad R_H = 150 \, \text{MPa}, \quad R_{pl} = 200 \, \text{MPa} \). Współczynniki wyboczeniowe przyjąć na podstawie znanych wyprowadzeń i podać ostatecznie wyznaczoną wartość siły krytycznej w kN.

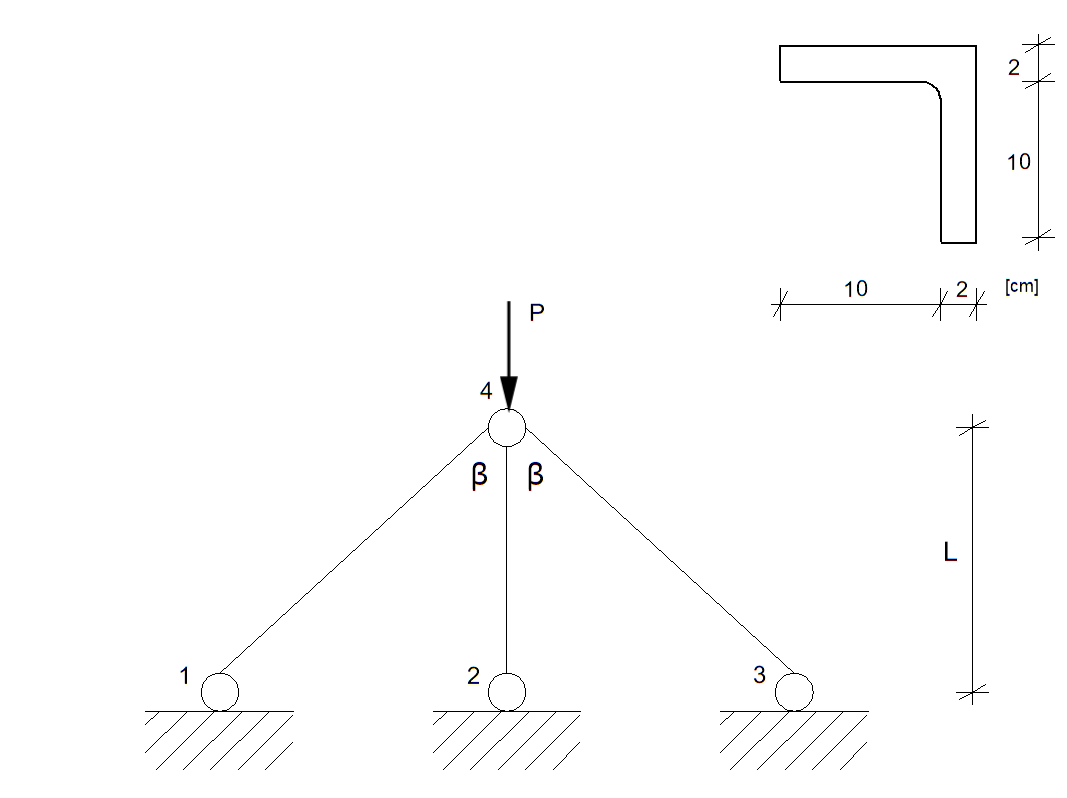
Dany jest układ złożony z prętów o przekroju podanym na rysunku.
Przyjmując \( E = 200\,\text{GPa}, \quad R_H = 200\,\text{MPa}, \quad R_{pl} = 240\,\text{MPa}, \quad l = 3\,\text{m}, \quad \beta = 45^\circ \) oraz krzywą wyboczeniową b, wyznaczyć nośność na ściskanie poszczególnych prętów układu wg wzoru empirycznego z PN-EN-1991-1-1:2006.

Następnie wyznaczyć maksymalną wartość siły \( P \), jaką można obciążyć dany układ prętowy, aby żaden z prętów nie uległ wyboczeniu.

Przyjąć, że wszystkie pręty w podanym układzie mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami stężonymi w kierunku prostopadłym do rysunku.

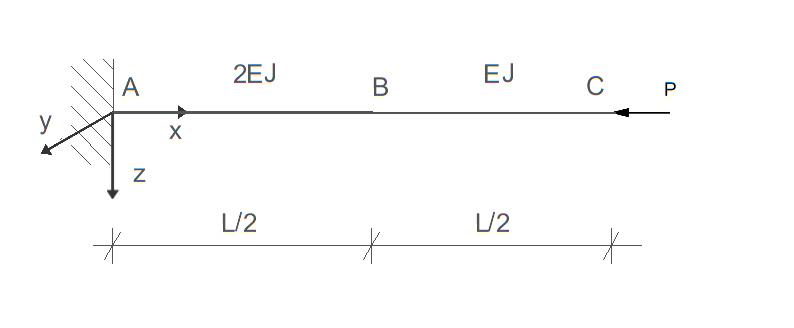
Przyjmując podane niżej przybliżone równanie osi odkształconej pręta osiowo ściskanego w chwili wyboczenia, korzystając z metody energetycznej, wyprowadzić wzór na siłę krytyczną. Parametry \( E, J, l, f \) przyjąć jako dane. \[ w(x) = f \left(1 - \cos\left( \frac{\pi x}{2l} \right) \right) \]

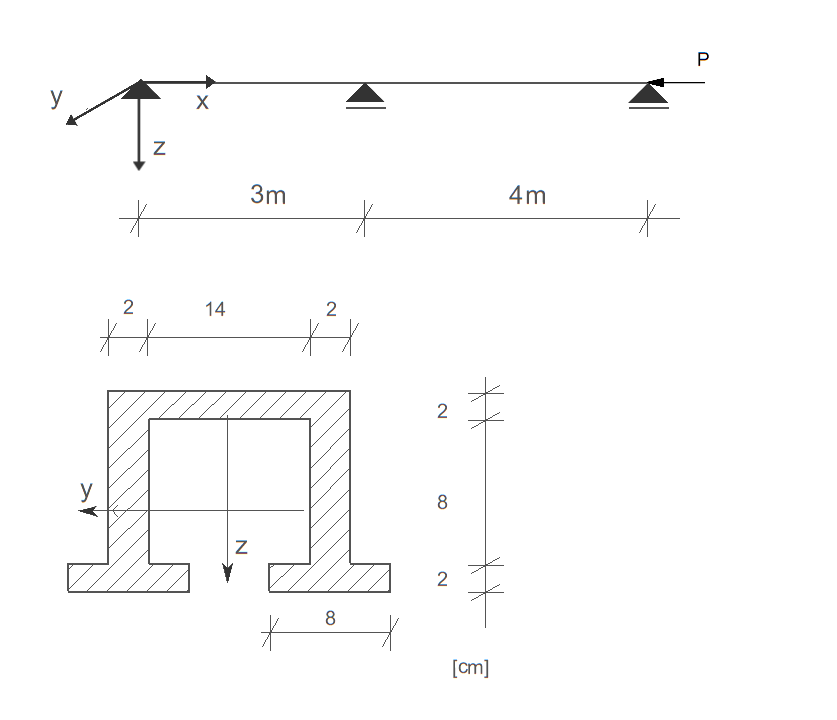
Dany jest pręt osiowo ściskany przedstawiony na rysunku.
Przyjmując \( E = 205 \, \text{GPa} \), \( R_H = 240 \, \text{MPa} \), \( R_{pl} = 300 \, \text{MPa} \), wyznaczyć wartość siły krytycznej danego pręta oraz przyjmując krzywą wyboczeniową c wyznaczyć nośność na ściskanie danego pręta wg wzoru empirycznego z PN-EN-1991-1-1:2006.

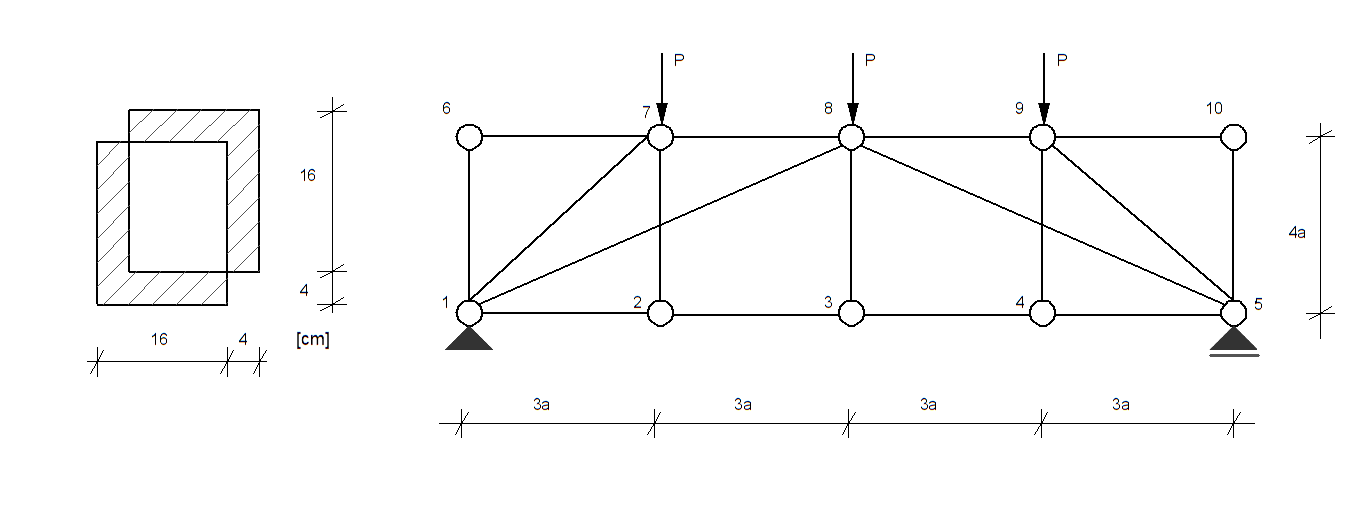
Dana jest kratownica wykonana z prętów o przekroju podanym na rysunku. Wyznaczyć maksymalną wartość siły P, jaką można obciążyć daną kratownicę, aby żaden z prętów nie uległ wyboczeniu. Przyjąć, że wszystkie pręty kratownicy mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami stężonymi w kierunku prostopadłym do kratownicy. Przyjąć: \( E = 80 \, \text{GPa}, \quad R_H = 200 \, \text{MPa}, \quad R_{pl} = 240 \, \text{MPa} \).

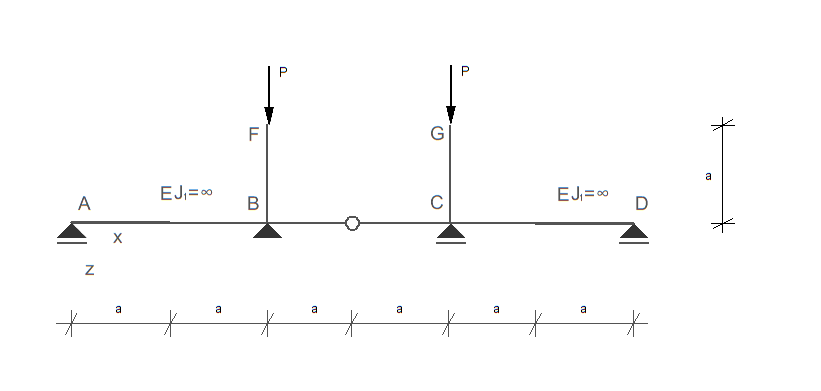
Korzystając z równania różniczkowego osi odkształconej (drugiego rzędu) wyprowadzić wzór na siłę krytyczną pręta ściskanego FB i GC. Przyjąć symetryczną postać wyboczenia.

Uwaga: Rozwiązaniem zadania jest wzór na siłę krytyczną w funkcji parametrów E, J i a.

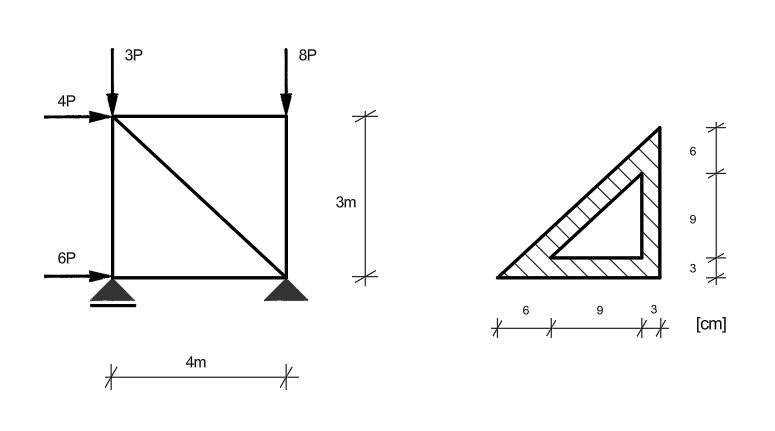
Jaką największą wartość może przyjąć \( P \), aby żaden z prętów danej kratownicy nie uległ wyboczeniu. Przyjąć, że wszystkie pręty kratownicy mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami kratownicy, które nie mogą doznać przemieszczeń prostopadłych do płaszczyzny kratownicy.

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

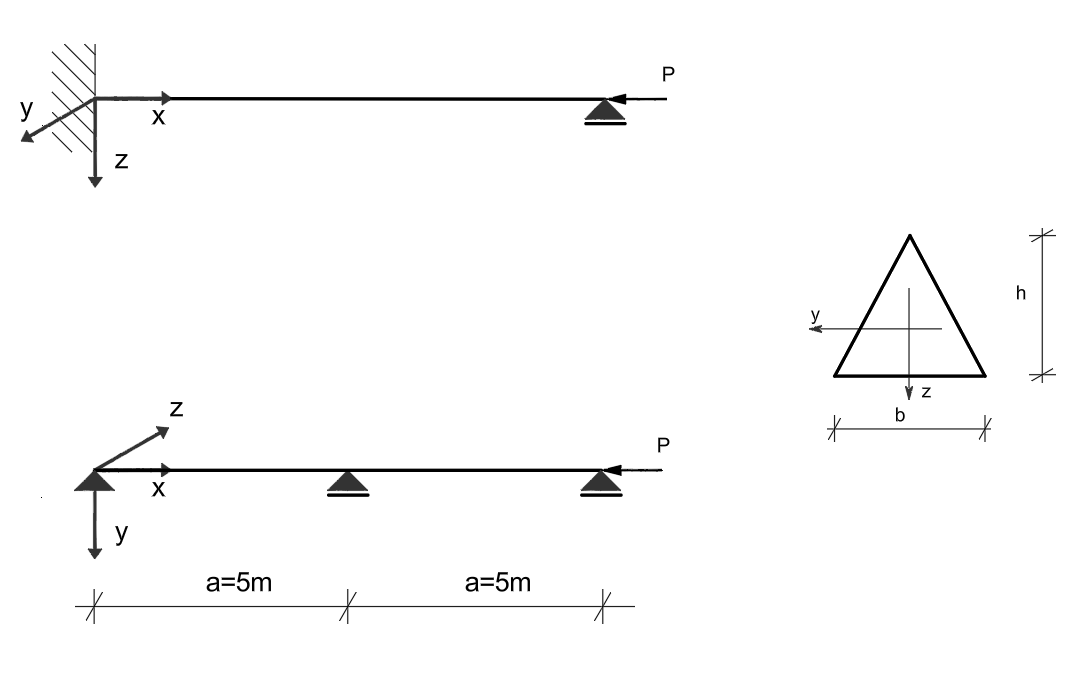
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach XY i XZ. Wyznaczyć wymiary \( b \) i \( h \) tak, aby tak aby niebezpieczeństwo wyboczenia w obu płaszczyznach było jednakowe i smukłość pręta odpowiadała smukłości granicznej.

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

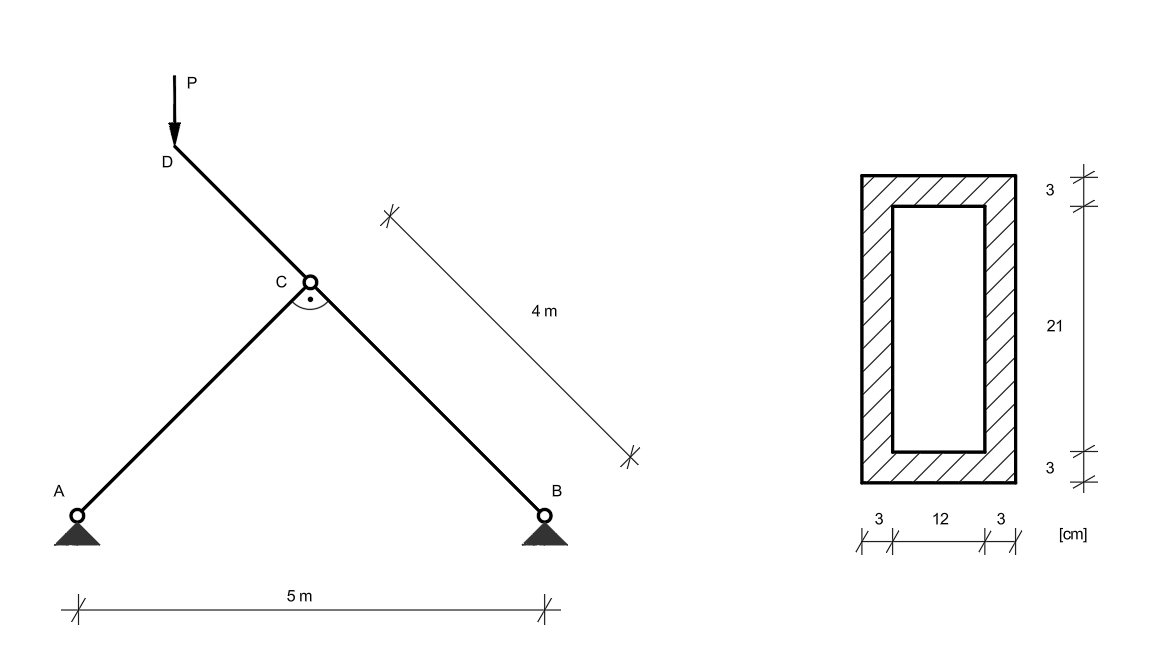
Jaką największą wartość może przyjąć siła \( P \), aby pręt AC nie uległ wyboczeniu. Przekrój pręta AC przyjąć w postaci rury o średnicy zewnętrznej \( D = 6\ \text{cm} \) i grubości ścianki \( g = 1\ \text{cm} \). Pręt BCD przyjąć w postaci podanej na poniższym rysunku. W obliczeniach przyjąć:

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

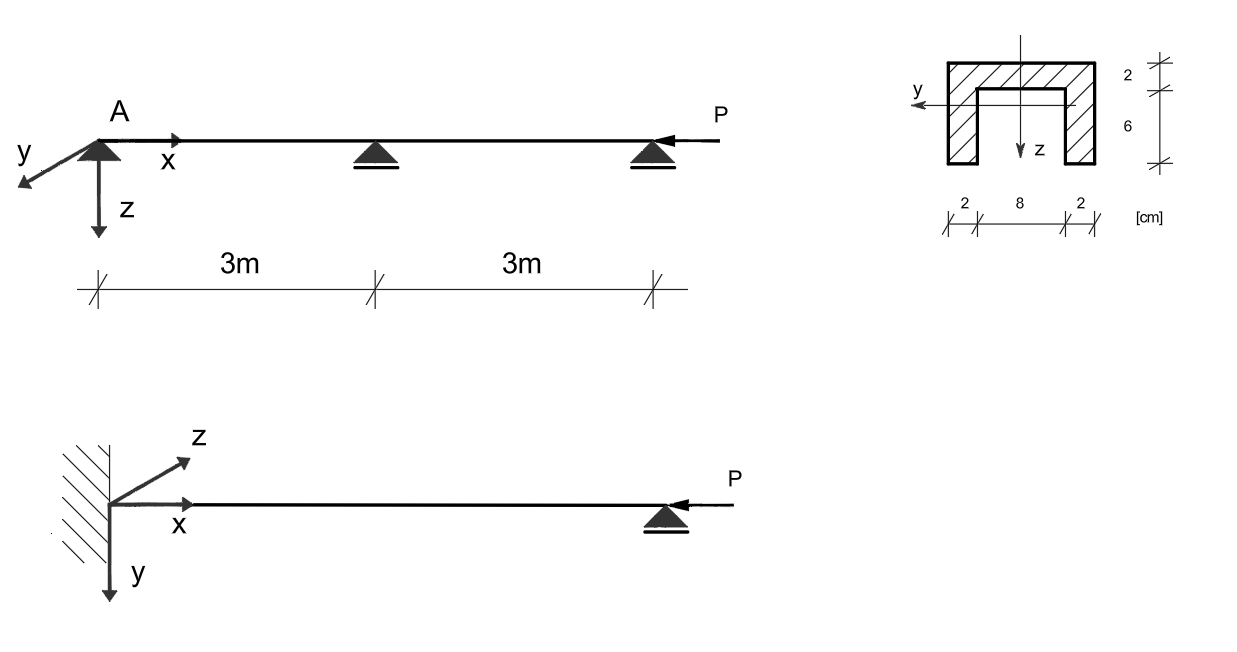
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach xy i xz, jak przedstawiono na poniższym rysunku. Przyjmując poniższe dane, wyznaczyć siłę krytyczną danego pręta:

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

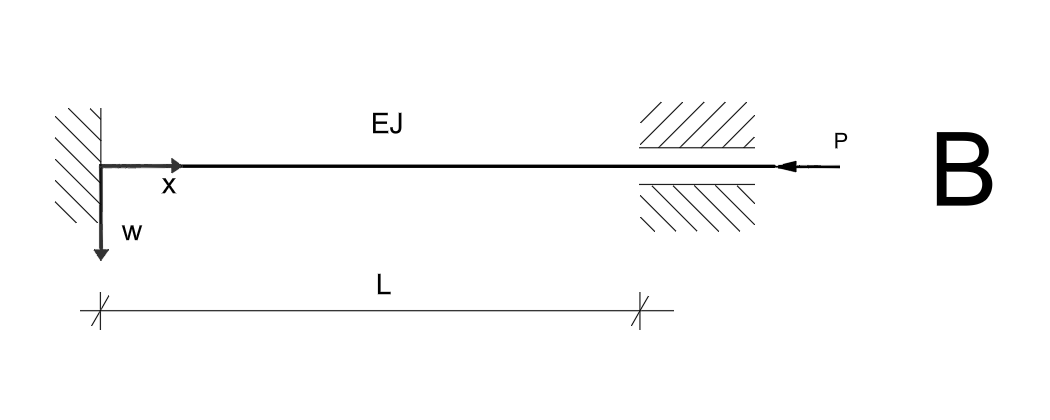
Przyjmując podane niżej przybliżone równanie osi odkształconej pręta osiowo ściskanego w chwili wyboczenia, wyznaczyć siłę krytyczną metodą energetyczną. Parametry \( E \), \( J \), \( I \) przyjąć jako dane.

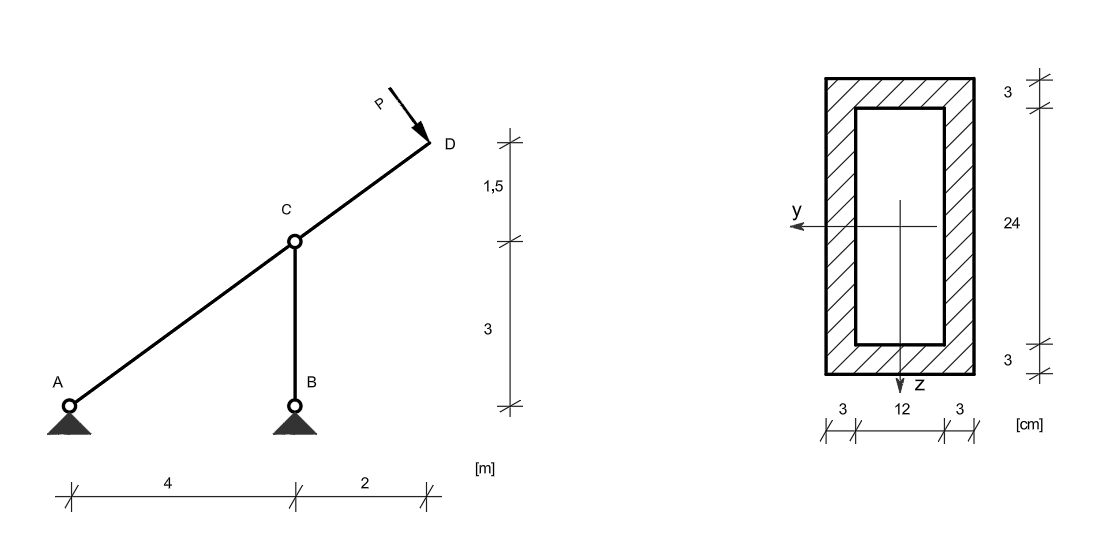
Jaką największą wartość może przyjąć siła \( P \), aby pręt CB nie uległ wyboczeniu. Przekrój pręta CB przyjąć w postaci rury o średnicy zewnętrznej \( D = 8\ \text{cm} \) i grubości ścianki \( g = 1\ \text{cm} \). Pręt ACD przyjąć w postaci podanej na poniższym rysunku. W obliczeniach przyjąć:

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

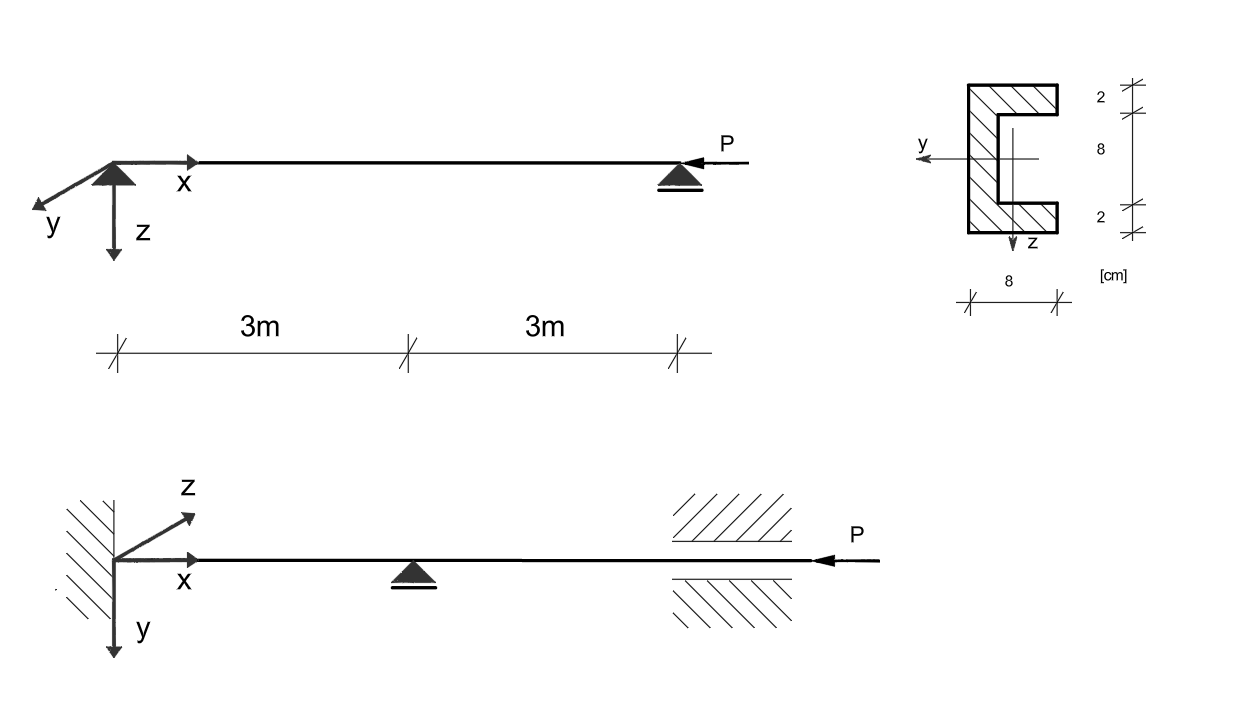
Dany jest pręt osiowo ściskany o różnych warunkach podparcia w płaszczyznach xy i yz, jak przedstawiono na poniższym rysunku. Przyjmując \( E = 205\ \text{GPa} \), \( R_H = 200\ \text{MPa} \) i \( R_e = 240\ \text{MPa} \) z zadania poprzedniego, wyznaczyć siłę krytyczną danego pręta.

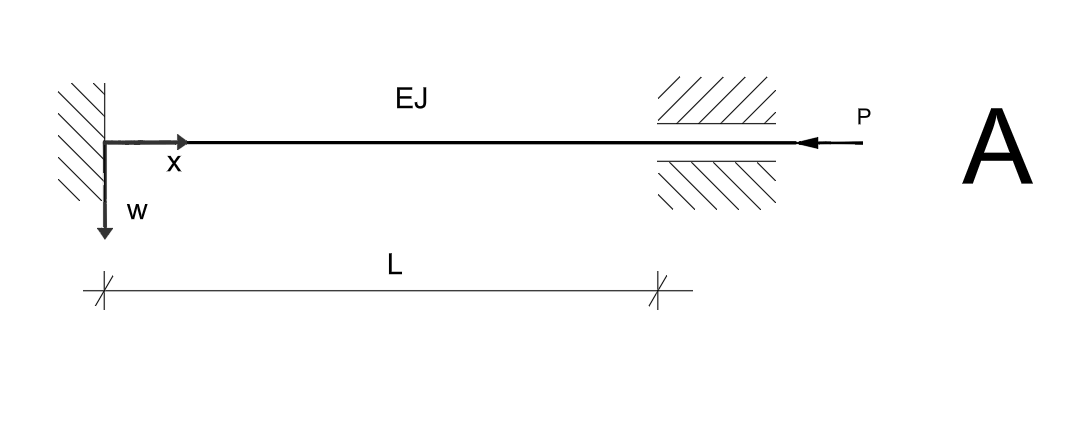
Przyjmując podane niżej przybliżone równanie osi odkształconej pręta osiowo ściskanego w chwili wyboczenia, wyznaczyć siłę krytyczną metodą energetyczną. Parametry \( E \), \( J \), \( I \) przyjąć jako dane.

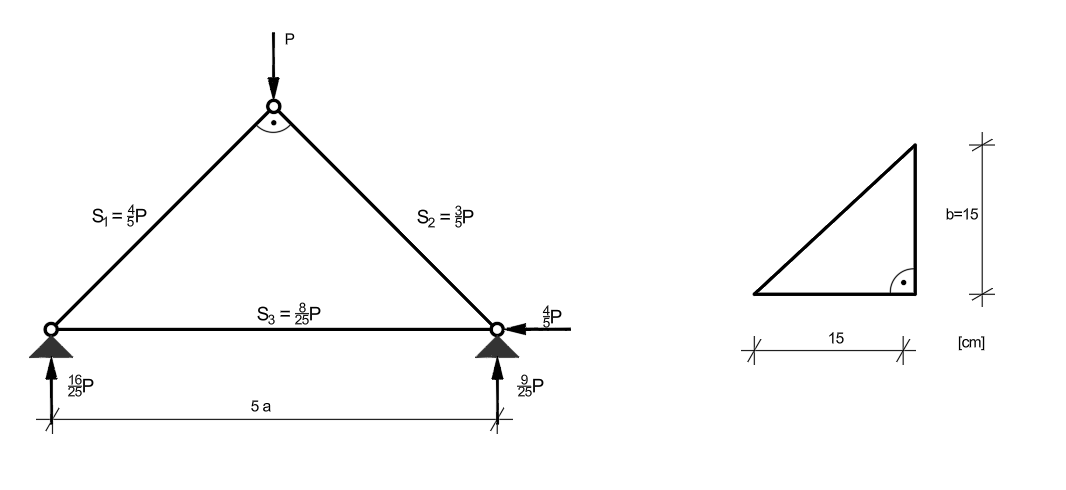
Jaką największą wartość może przyjąć \( P \), aby żaden z prętów podanego niżej układu nie uległ wyboczeniu. Wszystkie pręty mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko przegubami, które nie mogą wyjść z płaszczyzny układu. Wszystkie pręty mają przekrój podany niżej i wykonane są z materiału, dla którego:

• \( E = 205\ \text{GPa} \)
• \( R_H = 200\ \text{MPa} \)
• \( R_e = 240\ \text{MPa} \)

Ponadto przyjąć: \( \sin \alpha = 0{,}6 \), \( \cos \alpha = 0{,}8 \), \( a = 1\ \text{m} \).

Dany jest pręt zamocowany przegubowo do ścian, jak podano niżej na rysunku. Przyjmując, że pręt został zamocowany w temperaturze \( 10^\circ \text{C} \), wyznaczyć maksymalną wartość temperatury \( t \), przy której pręt nie ulegnie wyboczeniu.

Przekrój pręta przyjąć w postaci rury o średnicy zewnętrznej \( D = 7\ \text{cm} \) i grubości ścianki \( g = 1\ \text{cm} \).

Dane materiałowe przyjąć z zadania poprzedniego, a dodatkowo współczynnik rozszerzalności cieplnej \( \alpha_t = 0{,}000012\ 1/^\circ\text{C} \).

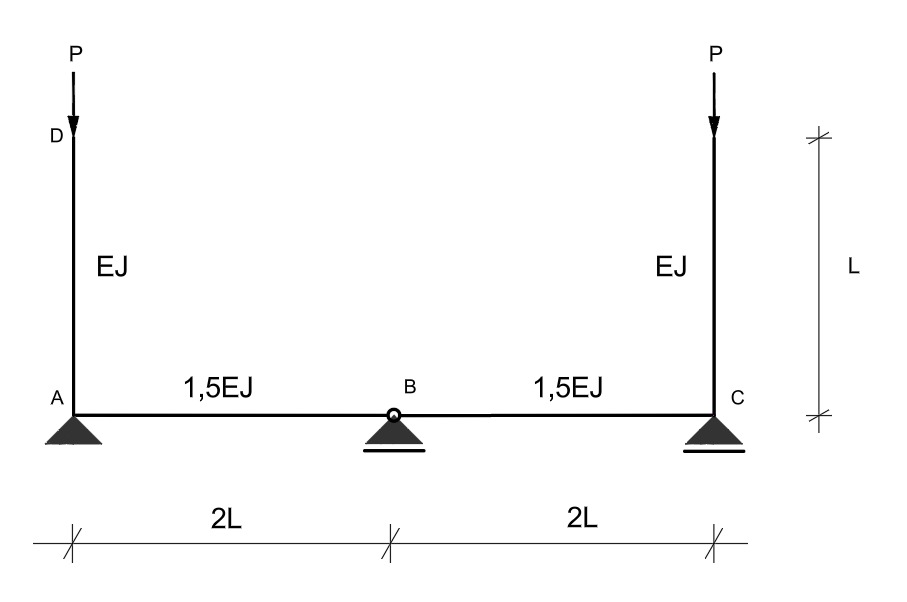
Korzystając z równania różniczkowego osi odkształconej pręta wyboczonego, wyznaczyć współczynnik wyboczeniowy \( \mu \) pręta AD. Wartości parametrów \( E \), \( I \), \( J \) należy przyjąć jako dane. Zadanie należy doprowadzić do jednego równania i na jego podstawie oszacować wartość współczynnika \( \mu \). Przyjąć symetryczną postać wyboczenia.

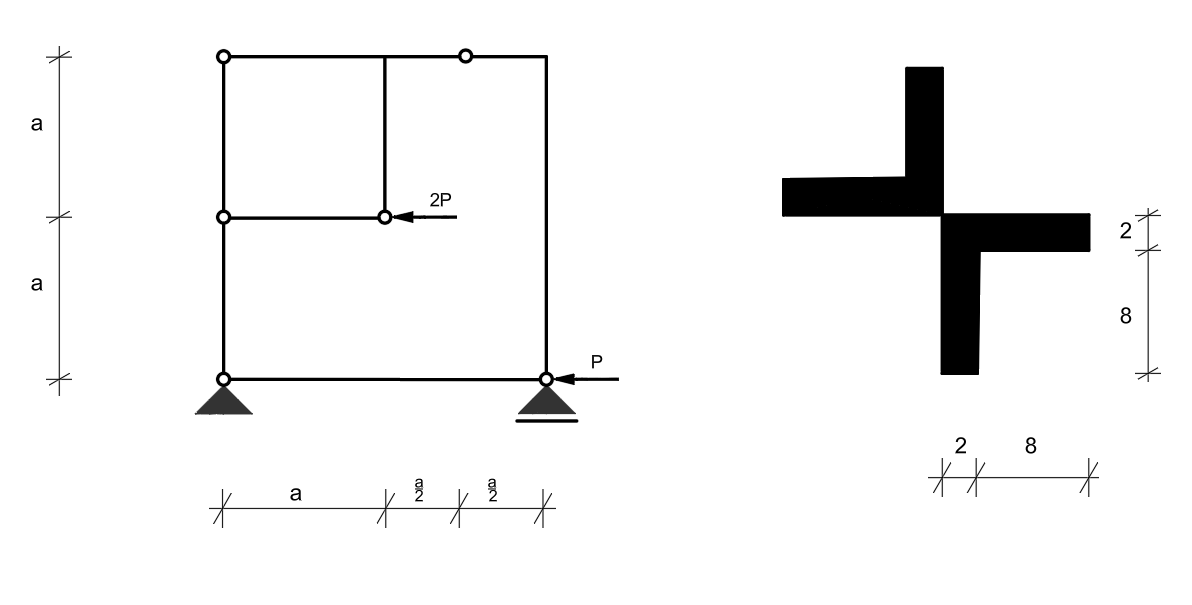
Jaką największą wartość może przyjąć obciążenie \( P \), przy którym pręty kratowe w danym układzie prętowym ulegną wyboczeniu. Przyjąć, że ten pręt mają swobodę wyboczenia w dowolnym kierunku, ograniczoną tylko węzłami, które są ściągnięte w kierunku prostopadłym do płaszczyzny układu.

Przyjąć: \( E = 205\ \text{GPa} \), \( R_H = 200\ \text{MPa} \), \( R_e = 240\ \text{MPa} \), \( a = 2,5m \).

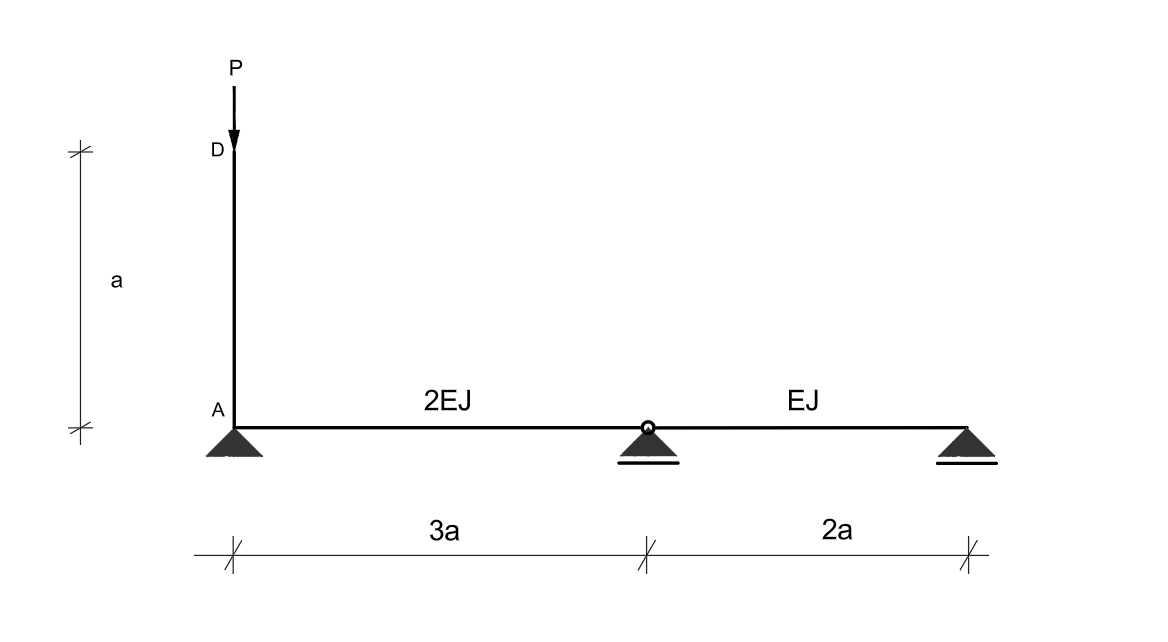
Korzystając z równania różniczkowego osi odkształconej, wyznaczyć współczynnik wyboczeniowy \( \mu \) pręta ściskanego AD.

Uwaga: Zadanie będzie uznane za rozwiązane, jeśli zostanie doprowadzone do jednego równania, z którego można wyznaczyć siłę krytyczną i współczynnik wyboczeniowy \( \mu \).