Lista zadań
Przykład 1

Pręt o zmiennej średnicy d oraz 2d jest utwierdzony na obu końcach i skręcany momentami \(M_0\) oraz \(3 M_0\), jak podano na poniższym rysunku. Wykonać wykres momentów skręcających, wykres naprężeń maksymalnych \(\tau_{max}\) oraz obliczyć kąt \(\varphi_C\) skręcenia przekroju C. Dane liczbowe l=1m, d=5cm, \(I_0=1000 cm^4\), G=80 GPa
Przykład 2

Jakie naprężenia powstaną w wałku stopniowym AB obustronnie utwierdzonym i obciążonym jak na rysunku? Dane: G = 60 GPa, dw = 4 cm, dz = 8 cm, d = 7 cm.
Przykład 3

Zwymiaruj średnicę pręta skręcanego momentem skręcającym 30 kNm, jeśli wytrzymałość na skręcanie wynosi \(k_s=70 MPa.\) Oblicz jakie naprężenia powstaną w tym pręcie, narysuj wykres momentów skręcających oraz kąta skręcenia. Dane: G = 80 GPa.
Przykład 4

Zwymiaruj średnicę pręta skręcanego momentem skręcającym 20 kNm, jeśli wytrzymałość na skręcanie wynosi ks=70 MPa. Oblicz jakie naprężenia powstaną w tym pręcie, narysuj wykres momentów skręcających oraz kąta skręcenia. Dane: E = 215 GPa, \(\nu =0,3\)
Przykład 5

Oblicz jakie naprężenia powstaną w tym pręcie, narysuj wykres momentów skręcających oraz kąta skręcenia. Dane: D = 25 cm, d = 20 cm, G = 80 GPa.
Przykład 6

Zwymiaruj średnicę pręta skręcanego momentem skręcającym 40 kNm, jeśli wytrzymałość na skręcanie wynosi ks=70 MPa. Oblicz jakie naprężenia powstaną w tym pręcie, narysuj wykres momentów skręcających, naprężeń stycznych oraz kąta skręcenia. Dane: G = 80 GPa.
Przykład 7

Oblicz maksymalny kąt skręcenia pręta danego na rysunku. Dane: D = 10 cm, d = 5 cm, G = 80 GPa.
Przykład 8

Jaki maksymalny moment skręcający M można przyłożyć do wałka o średnicach dz = 8 cm, dw = 4 cm, d = 6 cm, jeżeli dopuszczalne naprężenia wynoszą 120 MPa? G = 50 GPa.
Przykład 9

Jaki maksymalny moment skręcający M można przyłożyć do wałka o średnicach dz = 8 cm, dw = 4 cm, d = 6 cm, jeżeli dopuszczalne naprężenia wynoszą 120 MPa? G = 50 GPa.
Przykład 10
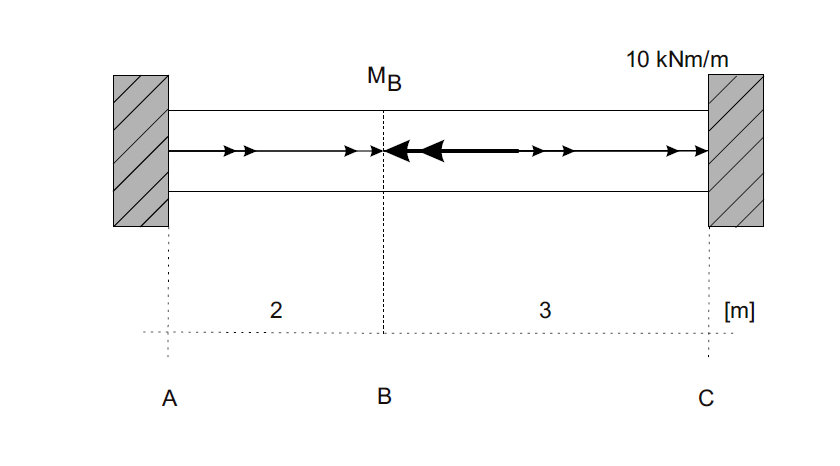
Treść zadania
Pręt o przekroju kołowym o średnicy \(d = 10 \text{ cm}\), wykonany jest z materiału o module ścinania \(G = 101,80 \text{ GPa}\). Oblicz moment bezwładności dla skręcanie przekroju poprzecznego: \(J_s\) w \([\text{cm}^4]\).
Dla obustronnie utwierdzonego pręta, obciążonego na całej długości równomiernie rozłożonym momentem o intensywności \(10 \text{ kNm/m}\) i momentem skupionym w przekroju \(B\) o wartości \(M_0 = 30 \text{ kNm}\), działającym przeciwnie niż moment rozłożony, narysuj wykresy:
\(M_s\) - momentów skręcających - sił przekrojowych i opisz w \([\text{kNm}]\).
\(\varphi\) - kątów obrotu względem utwierdzenia i opisz w \([10^{-3} \text{ rad}]\).
Uwaga: opisać ekstrema - czyli na rysunku zaznaczyć gdzie wystąpią i ile wyniosą. Oblicz maksymalną wartość naprężenia stycznego w tym pręcie: \(\tau_{\text{max}}\) \([\text{MPa}]\).
Przykład 11
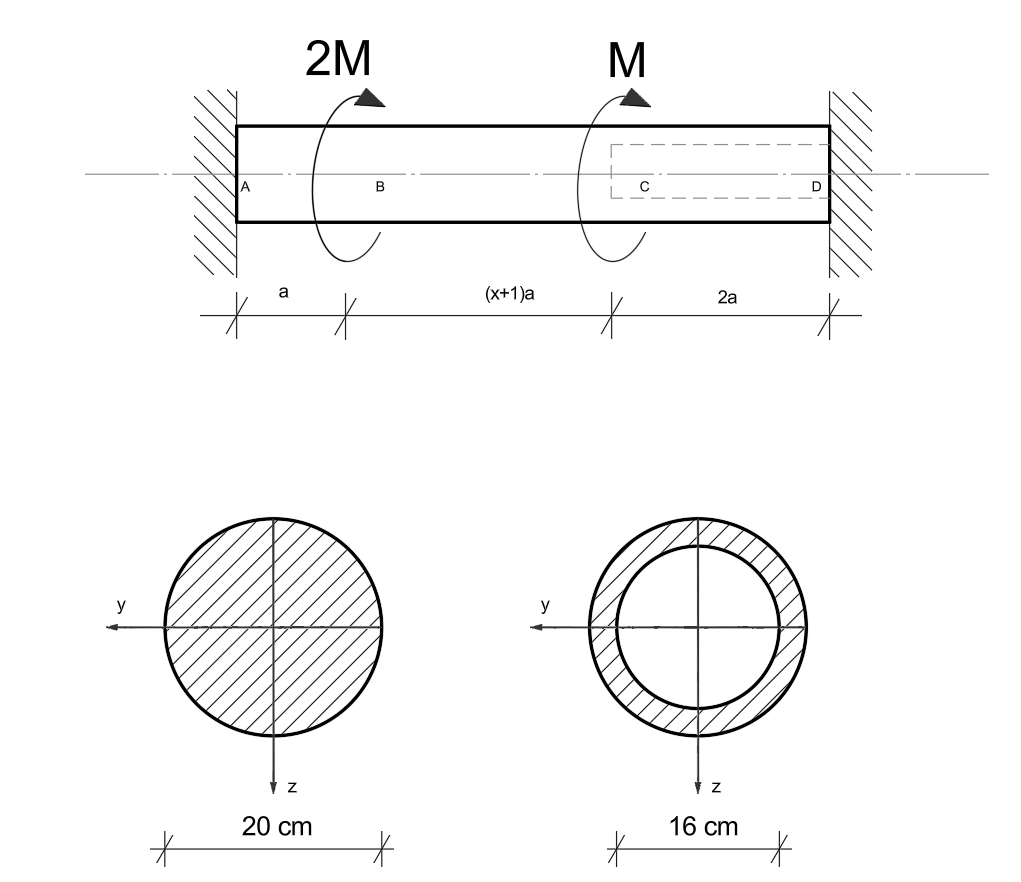
Wyznaczyć nośność sprężystą \( M = M_s \) i graniczną \( M = M_n \) podanego niżej pręta skręcanego. Wyznaczyć stosunek \( M_n / M_s \). Dla wyznaczonych wartości \( M_s \) i \( M_n \) sporządzić wykresy momentów skręcających. W obliczeniach przyjąć \( G = 26 \, \text{GPa} \), hipotezę Treski i podane wyżej wartości \( a \) i \( R_{pl} \) (przy rozciąganiu).