Rozwiązanie
Układy niewyznaczalne Metodą Clebscha rozwiązuje się właściwie tak samo jak przemieszczenia w układach wyznaczalnych, z tą różnicą że jest jedno więcej równanie (warunek brzegowy) i jedna więcej niewiadoma (reakcja).
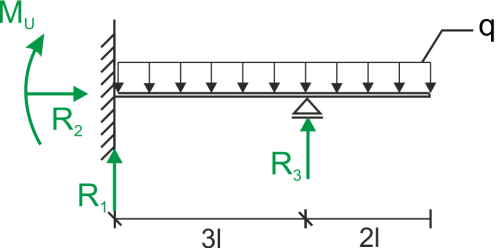
Metoda Clebscha
Równania równowagi
\begin{aligned}\\ &\sum{X}=0\\ & R_2=0\\ &\sum{Y}=0 \\ &R_1+R_3-5ql=0 \\ &R_1=5ql-R_3\\ &\sum{M_1}=0 \\ &M_U-R_3*3l+\frac{25}{2}ql^2=0 \\ &M_U=3lR_3-\frac{25}{2}ql^2\\ \end{aligned}Klasyczna Metoda Clebscha
\begin{aligned}\\ &M_g=M_u*x^0+R_1x-\frac{1}{2}qx^2+R_3(x-3l)\\ &M_g=3R_3lx^0-\frac{25}{2}ql^2x^0+5qlx-R_3x-\frac{1}{2}qx^2+R_3(x-3l)\\ &EIw''=-M_g\\ &EIw''=-3R_3lx^0+\frac{25}{2}ql^2x^0-5qlx+R_3x+\frac{1}{2}qx^2-R_3(x-3l)\\ &EIw'=-3R_3lx+\frac{25}{2}ql^2x-5ql\frac{x^2}{2}+R_3\frac{x^2}{2}+\frac{1}{2}q\frac{x^3}{3}-R_3\frac{(x-3l)^2}{2}+C\\ &EIw=-3R_3l\frac{x^2}{2}+\frac{25}{2}ql^2\frac{x^2}{2}-5ql\frac{x^3}{6}+R_3\frac{x^3}{6}+\frac{1}{2}q\frac{x^4}{12}-R_3\frac{(x-3l)^3}{6}+Cx+D\\ \end{aligned}Warunki brzegowe
\begin{aligned}\\ &w'_{(0)}=0 \\ &C=0\\ &w_{(0)}=0 \\ &D=0\\ &w_{(3l)}=0\\ &-3R_3l\frac{3^2}{2}l^2+\frac{25}{2}ql^2\frac{3^2*l^2}{2}-5ql\frac{3^3*l^3}{6}+R_3\frac{3^3*l^3}{3}+\frac{1}{2}q\frac{3^4*l^4}{12}=0\\ &-9R_3l^3+\frac{297}{8}ql^4=0\\ \end{aligned}Reakcje
\begin{aligned}\\ &R_3=\frac{33}{8}ql \\ &R_1=\frac{7}{8}ql \\ &M_U=-\frac{1}{8}ql^2\\ \end{aligned}
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB:
