Wytrzymałość materiałów - Metoda mohra
Metoda Mohra, znana również jako metoda grafo-analityczna, metoda belki zastępczej, metoda obciążenia wtórnego lub metoda graficzna, opiera się na dwuetapowym podejściu do rozwiązania
problemu określenia rozkładu momentów zginających w belce.
W pierwszym kroku zajmujemy się standardowym rozkładem sił przekrojowych w konkretnej (zadanej) belce. Następnie, w drugim etapie, koncentrujemy się na ustaleniu rozkładu momentów w tzw. "belce zastępczej".
Dla belki zastępczej (wtórnej, fikcyjnej) dobieramy geometrię, podparcie i obciążenie w taki sposób, aby, opierając się na rozwiązaniu pierwszego etapu, uzyskać rozkład momentów, który jest liczbowo identyczny z rozkładem ugięć w rzeczywistej belce.
Żeby lepiej zrozumieć zobacz poniższy przykład


Będą one równe odpowiednim przemieszczeniom w tym samym punkcie osi belki rzeczywistej.
-> Sile tnącej w punkcie K na belce fikcyjnej odpowiada kąt obrotu punktu K belki rzeczywistej,
-> Momentowi gnącemu w punkcie K na belce fikcyjnej odpowiada ugięcie belki rzeczywistej w tym punkcie.
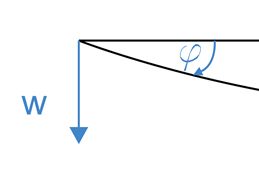
W przyjętym układzie odniesienia ugięcie w>0 jest skierowane w dół belki, a dodatni kąt obrotu \(\varphi>0\) będzie zgodny z ruchem wskazówek zegara.
Zamiana belki rzeczywistej na belkę fikcyjną
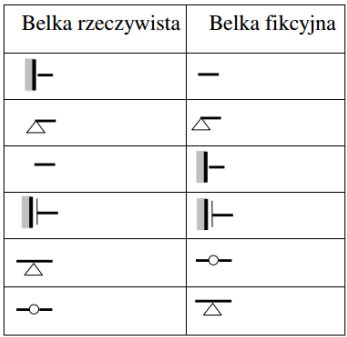
- jak wyznaczyć wykres momentów gnących,
- jak określić podparcie belki fikcyjnej (wtórnej),
- jak obciążyć belkę wtórną,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Projektowanie na ugięcie:
- jak zwymiarować przekrój belki z warunku użytkowalności (na dopuszczalne ugięcie),
- jak wyznaczyć wartość dopuszczalnego obciążenia mając zadany przekrój.
W pierwszym kroku zajmujemy się standardowym rozkładem sił przekrojowych w konkretnej (zadanej) belce. Następnie, w drugim etapie, koncentrujemy się na ustaleniu rozkładu momentów w tzw. "belce zastępczej".
Dla belki zastępczej (wtórnej, fikcyjnej) dobieramy geometrię, podparcie i obciążenie w taki sposób, aby, opierając się na rozwiązaniu pierwszego etapu, uzyskać rozkład momentów, który jest liczbowo identyczny z rozkładem ugięć w rzeczywistej belce.
Żeby lepiej zrozumieć zobacz poniższy przykład
Algorytm
Tok postępowania przy rozwiązaniu zadania
• wyznaczyć wykres momentów zginających w belce rzeczywistej (przyjmując spody na dole belki),
• wyznaczyć belkę fikcyjną/wtórną (zgodnie z tabelą poniżej),
• obciążyć belkę fikcyjną/wtórną wykresem momentów zginających z belki rzeczywistej podzielonemu przez jej sztywność na zginanie EI.

• wyznaczyć siłę poprzeczną i/lub moment zginający w tym wybranym punkcie w belce fikcyjnej, znakowanie:

Będą one równe odpowiednim przemieszczeniom w tym samym punkcie osi belki rzeczywistej.
-> Sile tnącej w punkcie K na belce fikcyjnej odpowiada kąt obrotu punktu K belki rzeczywistej,
\(\varphi(x)=Q_f (x) \)
-> Momentowi gnącemu w punkcie K na belce fikcyjnej odpowiada ugięcie belki rzeczywistej w tym punkcie.
\( w(x)=M_f (x)\)
W przyjętym układzie odniesienia ugięcie w>0 jest skierowane w dół belki, a dodatni kąt obrotu \(\varphi>0\) będzie zgodny z ruchem wskazówek zegara.

Z tego kursu dowiesz się
Metoda Mohra (grafoanalityczna):- jak wyznaczyć wykres momentów gnących,
- jak określić podparcie belki fikcyjnej (wtórnej),
- jak obciążyć belkę wtórną,
- jak obliczyć ugięcie i kąt obrotu belki w dowolnym punkcie.
Projektowanie na ugięcie:
- jak zwymiarować przekrój belki z warunku użytkowalności (na dopuszczalne ugięcie),
- jak wyznaczyć wartość dopuszczalnego obciążenia mając zadany przekrój.
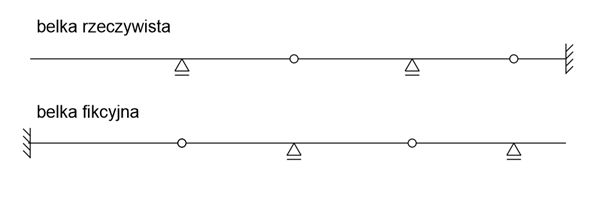
Przykład - Metoda Mohra - zamiana podpór z belki pierwotnej na wtórną
Rozwiązanie
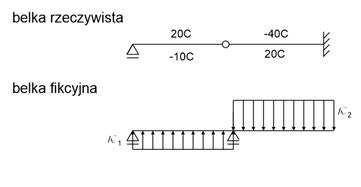
Przykład - Metoda Mohra - wpływ temperatury
Rozwiązanie
Oczywiście metodą Mohra można również obliczyć przemieszczenie od wpływu temperatury. Korzystamy ze wzoru:\(\kappa=\frac{\alpha \Delta T}{h}\)
Wówczas obciążenie belki fikcyjnej ma wartość κ i jest skierowane w stronę włókien cieplejszych.
Przykład - wideo kurs
Rozwiązanie zadania w trakcie korepetycji online
ZOBACZ TEŻ

