Edupanda » Wytrzymałość materiałów » Rozciąganie i ściskanie osiowe

Rozciąganie i ściskanie osiowe

Z tego tekstu dowiesz się:
- kiedy mamy do czynienia z rozciąganiem
- o konwencji dodatniego znakowania siły normalnej
- czym jest i jaki jest wzór na:
a) wydłużenie pręta
b) odkształcenia pręta rozciąganego
c) naprężenia normalne
- czym jest liczba Poissona
- jaka jest postać tensora naprężenia i odkształcenia dla pręta rozciąganego
- jak obliczyć energię sprężystą dla pręta rozciąganego
- jak wygląda kostka naprężeń oraz koło Mohra dla przypadku rozciągania osiowego

Znajdziesz również przykłady obliczeniowe i kursy wideo na dole strony oraz

↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓

Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz 4 zadania z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz 17 zadań z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz 11 zadań z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz zadania z użyciem podstawowych definicji


Kiedy mamy do czynienia z rozciąganiem osiowym?

Rozciąganie/ściskanie osiowe pręta występuje, gdy wszystkie siły działające na przekrój poprzeczny z jednej strony sumują się w taki sposób, że tworzą pojedynczą siłę skierowaną prostopadle do przekroju. Ta siła działa wzdłuż osi pręta i jest zaczepiona w jego środku ciężkości.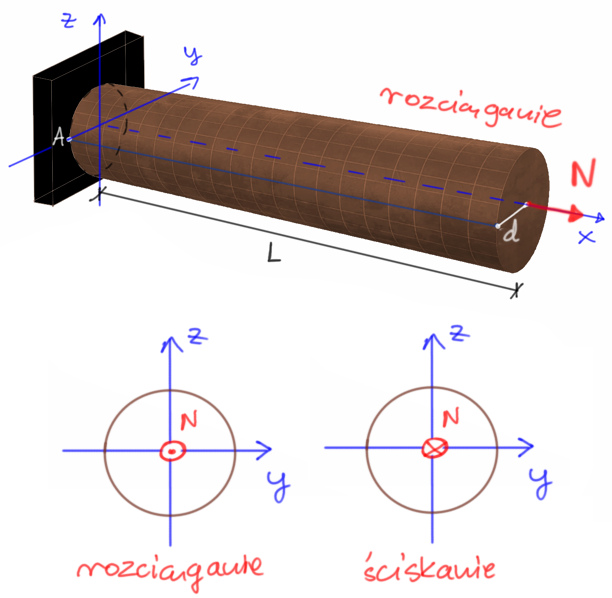
rozciaganie osiowe

Rys1. Rozciąganie osiowe pręta kołowego


Konwencja dodatniego znakowania siły normalnej

Jeśli kierunek działania tej siły jest taki sam jak normalna (prostopadła) do powierzchni zewnętrznej pręta, nazywamy ją siłą rozciągającą, a jej wartości przypisujemy znak dodatni.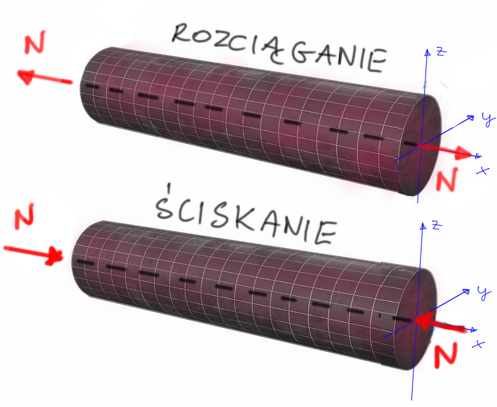
Znakowanie sił normalnych/osiowych

Rys2. Znakowanie sił normalnych/osiowych


Wydłużenie pręta albo jego części obliczamy tak:

Całkowita zmiana długości pręta jest całką oznaczoną (po długości) z funkcji odkształceń podłużnych:
\[ \Delta l=\int_0^l \varepsilon_x d x=\int_0^l \frac{N(x)}{E A} d x \] Jeżeli mamy do czynienia z prętem jednorodnym o określonej sztywności na rozciąganie (\(EA=\) const \()\) poddanym działaniu siły normalnej o stałej wartości \((N=\) const \()\), a nie funkcją siły normalnej, która może być związana choćby z uwzględnieniem ciężaru własnego, to otrzymujemy:
\[ \Delta l=\int_0^l \frac{N}{E A} d x=\frac{N}{E A} \int_0^l d x=\frac{N l}{E A} . \]
gdzie:
N - siła normalna lub N(x) - funkcja siły normalnej
l - długość pręta, lub części pręta
E - moduł Younga (stała materiałowa)
A - pole przekroju poprzecznego

Odkształcenia pręta rozciąganego

a) wpływ obciążenia statycznego
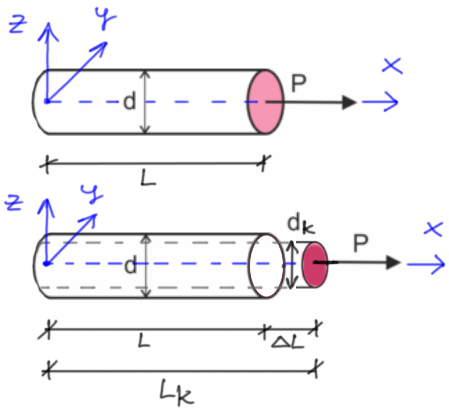
Wydłużenie pręta i zmiana wymiarów

Rys3. Wydłużenie pręta i zmiana wymiarów


Odkształcenie podłużne \( \varepsilon_x \) oraz odkształcenia poprzeczne \( \varepsilon_y , \varepsilon_z \)
obliczymy w następujący sposób:
\[ \varepsilon_x=\frac{\Delta L}{L}=\frac{L_k-L}{L} \] \[ \varepsilon_y=\frac{\Delta d}{d}=\frac{d_k-d}{d} \] \[ \varepsilon_z=\frac{\Delta d}{d}=\frac{d_k-d}{d} \]
b) wpływ obciążenia pozastatycznego
Pręt może zmieniać swoją długość również ze względu na oddziaływania pozastatyczne, takie jak równomierne podgrzewanie pręta w stosunku do jego temperatury początkowej (temperatury montażu). Odkształcenia termiczne które powstają w pręcie od obciążenia równomiernym podgrzaniem lub oziębieniem pręta wyrażamy wzorem: \[ \varepsilon_{x(T)}=\alpha_t \cdot t_0 \] \( \quad \) gdzie:
\( \quad \) - \(t_0\) - różnica temperatury pręta w porównaniu do jego pierwotnej temperatury wyrażona w kelwinach \( [K] \) lub stopniach Celsjusza \( [^oC] \) (różnica temperatur w obu skalach zawsze jest taka sama)
\( \quad \) - \( \alpha_t \) - współczynnik rozszerzalności termicznej, definiowany jako jednostkowa zmiana długości wywołana zmianą temperatury o \( 1K / 1^oC \) wyrażona w \( \frac{1}{K} \) lub \( \frac{1}{^oC} \)

Zmianę długości pręta o długości \(l\) pod działaniem równomiernej temperatury wyrazimy wzorem: \[ \Delta l_T=\varepsilon_{x(T)} \cdot l=\alpha_t \cdot t_0 \cdot l \] A więc jeżeli na pręt działa obciążenia statyczne i termiczne, wówczas możemy zapisać: \[ \Delta l=\Delta l_N+\Delta l_T=\int_0^l \frac{N(x)}{E A} d x+ \alpha_t \cdot t_0 \cdot l \]
Zależności między odkształceniami podłużnymi i poprzecznymi określa Liczba Poissona
Zmianę objętości obliczymy z zależności: \( \Delta V=(ε_x+ε_y+ε_z)\cdot V \)
V - objętość początkowa pręta

Liczba Poissona

Liczba Poissona to materiałowa stała fizyczna, która opisuje związek między odkształceniem poprzecznym (zmianą szerokości) a odkształceniem podłużnym (zmianą długości) w materiale.
Konkretniej, liczba Poissona (najczęściej oznaczana symbolem \( \nu \) ) jest stosunkiem względnego odkształcenia poprzecznego do względnego odkształcenia podłużnego w materiale.
Wyraża się ją jako:
\[ \nu = - \frac{ε_{poprzeczne}}{ε_{podłużne}} \] gdzie:
\( \quad \nu \) to liczba Poissona,
\( \quad ε_{poprzeczne} \) to względne odkształcenie poprzeczne,
\( \quad ε_{podłużne} \) to względne odkształcenie podłużne.

w przykładzie powyżej zapisalibyśmy:
\[ \nu = - \frac{ε_y}{ε_x} \] \[ \nu = - \frac{ε_z}{ε_x} \] lub przekształcając:
\[ ε_y = - \nu \cdot ε_x \] \[ ε_z = - \nu \cdot ε_x \] Liczba Poissona jest ważna w analizie wytrzymałości materiałów, ponieważ pozwala określić, w jaki sposób materiał zachowuje się pod obciążeniem, zwłaszcza w kontekście jego elastyczności i odporności na odkształcenia.
Różne materiały mają różne liczby Poissona, co wpływa na ich właściwości mechaniczne i zachowanie pod obciążeniem. Na przykład, dla niektórych materiałów ν jest bliskie 0, co oznacza, że zmiany w jednym kierunku (poprzecznym) są praktycznie niezauważalne w przypadku odkształceń w innym kierunku (podłużnym).
W innych materiałach ν może być większe, co oznacza większą zmienność w tych odkształceniach.

Naprężenia normalne

Rozkład naprężeń normalnych
Rys4. Rozkład naprężeń normalnych


Wzór na naprężenia normalne przy rozciąganiu/ściskaniu osiowym w dowolnym punkcie przekroju poprzecznego wygląda następująco: \[ \sigma=\frac{N}{A} \] gdzie:
N - siła normalna (osiowa),
A - pole przekroju poprzecznego pręta.

Postać tensora naprężenia i odkształcenia dla pręta rozciąganego/ściskanego osiowo:

\begin{aligned} T_\sigma=\left[\begin{array}{ccc} \sigma_x & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \quad T_{\varepsilon}=\left[\begin{array}{ccc} \varepsilon_x & 0 & 0 \\ 0 & \varepsilon_y & 0 \\ 0 & 0 & \varepsilon_z \end{array}\right] \end{aligned}

Energia sprężysta dla pręta rozciąganego/ściskanego osiowo

Dla pręta o jednym przedziale charakterystycznym: \[U=\int_0^L \frac{N^2(x)}{2 E A} d x\] Dla pręta o większej liczbie przedziałów (jeśli zmienia się na długości pręta przekrój lub materiał lub jeżeli w różnych miejscach mamy obciążenie siłami osiowymi) wówczas musimy zrobić sumowanie po wszystkich przedziałach charakterystycznych: \[U=\sum_{i=1}^n \int_0^{L_i} \frac{N_i^2(x)}{2 E_i A_i} d x\]

Kostka naprężeń dla przypadku rozciągania/ściskania osiowego, naprężenia i kierunki główne, koło Mohra

Jeżeli mamy do czynienia z rozciąganiem, wówczas naprężenie \( \sigma_1=\frac{N}{A} \) jest to maksymalne naprężenie, a więc główne. Minimalne naprężenia jest równe \( \sigma_2=0 \).
Jeżeli mamy do czynienia ze ściskaniem, wówczas naprężenie \( \sigma_2=\frac{-N}{A} \) jest to minimalne naprężenie, a więc główne. Maksymalne naprężenia jest równe \( \sigma_1=0 \).
Naprężenia styczne są równe 0.

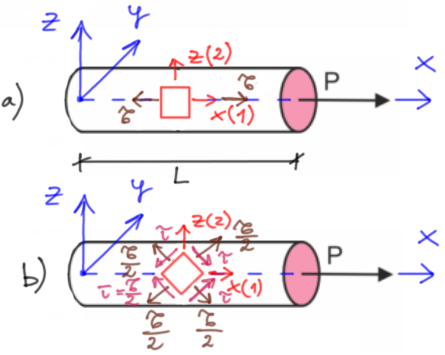
Kostki naprężeń rozciąganie

Rys5. Kostki naprężeń przy rozciąganiu
a) naprężenia główne
b) kostka obrócona o 45 stopni - stan z maksymalnymi naprężeniami stycznymi


Rozważmy jednak jeszcze przekrój nachylony pod kątem \( 45^o \) do osi pręta, ponieważ w tym przekroju występują w pręcie rozciąganym/ściskanym maksymalne naprężenia styczne.
Wzór na maksymalne i minimalne naprężenia styczne w płaskim stanie naprężenia: \[ \begin{aligned} & \tau_{\max }=\frac{\sigma_{1}-\sigma_{2}}{2}=\frac{\sigma}{2}, \\ & \tau_{\min }=-\frac{\sigma_{1}-\sigma_{2}}{2}=\frac{- \sigma}{2} \end{aligned} \] Skąd wiemy, że maksymalne naprężenie styczne w tym przypadku wystąpi pod kątem \( 45^o \)?
Jeśli wiemy, że wartość maksymalnego naprężenia stycznego wynosi \( \tau_{max}=\frac{\sigma}{2} \) oraz że \( \sigma_1=\sigma \) i \( \sigma_2=0 \), gdzie \( \sigma=\frac{N}{A} \) to skorzystamy ze wzoru opisującego stan naprężenia w przekroju nachylonym pod kątem \( \alpha \) do kierunku większego naprężenia głównego: \[ \tau_\alpha=\frac{\sigma_1-\sigma_2}{2} \cdot \sin (2 \alpha) \] podstawiamy dane: \[ \frac{\sigma}{2}=\frac{\sigma-0}{2} \cdot \sin (2 \alpha) \quad |:\frac{\sigma}{2} \\ 1=\sin (2 \alpha) \quad | asin ( ) \\ asin (1) = 2 \alpha \\ 90^o = 2 \alpha \\ \alpha = 45^o \] Jakie są w takim razie naprężenia normalne w przekroju obróconym o \( 45^o \)? Określa to wzór: \[ \sigma_\alpha=\sigma_1 \cos ^2 \alpha+\sigma_2 \sin ^2 \alpha=\frac{\sigma_1+\sigma_2}{2}+\frac{\sigma_1-\sigma_2}{2} \cos (2 \alpha) \] podstawiamy dane: \[ \sigma_\alpha=\sigma \cos ^2 (45^o) +0 \cdot \sin ^2 \alpha=\frac{\sigma}{2} \]

koło Mohra

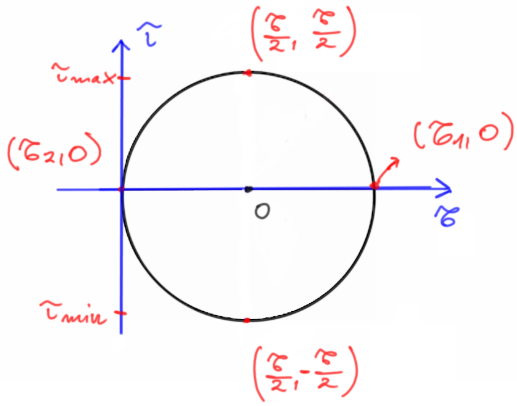
Koło Mohra - rozciąganie osiowe

Rys6. Koło Mohra - rozciąganie osiowe


↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓

Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz 4 zadania z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz 17 zadań z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz 11 zadań z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz zadania z użyciem podstawowych definicji



Przejdźmy teraz z teorii do praktyki

Z tego działu mamy bardzo dużo darmowych kursów wideo, które znajdziesz poniżej.
Naciśnij napis pod miniaturą poniżej aby przewinąć do zadania które Cię interesuje.

Pojedyncze pręty - układy statycznie wyznaczalne Układy prętów - statycznie wyznaczalne Zadania statycznie niewyznaczalne
ZADANIE 1 ZADANIE 4 ZADANIE 7
ZADANIE 2 ZADANIE 5 ZADANIE 8
ZADANIE 3 ZADANIE 6 ZADANIE 9

Zobacz ofertę i cenę korepetycji

Łukasz Cichowicz
Tel: +48 780 155 029
E-mail: lukasz@edupanda.pl
Skype: edupandapl

Przykład 1

Treść

Dwustopniowy pręt został trwale utwierdzony końcem A i obciążony siłami P oraz 2P jak na rysunku. Obliczyć średnicę obu prętów, znając naprężenia dopuszczalne na ściskanie i rozciąganie.Narysować wykresy sił wewnętrznych, naprężeń normalnych oraz wydłużeń i przemieszczeń pręta.
Dane: \(P=10 kN, E=2,1\cdot 10^{5} MPa, a=1 m, k_{r}=60 MPa, k_{c}=80 MPa\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć
Obliczenie rekacji
\begin{aligned} &\sum X=0 \\ &R_{A}+2 P-P=0 \\ &R_{A}=-P \\ \end{aligned} Zapisanie sił normalnych na przedziałach charakterystycznych
\begin{aligned} &N_{1}=-P=-10 k N \\ &N_{2}=-P=-10 k N \\ &N_{3}=-P+2 P=P=10 k N \\ \end{aligned} Warunek wytrzymałości
\begin{aligned} &\sigma=\left|\frac{N}{A}\right| \leq k_{r}, k_{c} \end{aligned} Ściskanie \begin{aligned} &\frac{10 \cdot 10^{3}}{A} \leq 80 \cdot 10^{6} \\ &A \geq \frac{10 \cdot 10^{3}}{80 \cdot 10^{6}} \\ &A \geq 1,25 \cdot 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned}

Rozciąganie

\begin{aligned} &\frac{10 \cdot 10^3}{2 A} \leq 60 \cdot 10^{6} \\ &2 A \geq \frac{10 \cdot 10^{3}}{60 \cdot 10^{6}} \\ &A \geq 8,33 \cdot 10^{-5}=0,833 \cdot 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned} Decyduje warunek na rozciąganie. Wymiarowanie średnicy: \begin{aligned} &A \geq 1,25 \cdot 10^{-4} \\ &\frac{\pi d^{2}}{4} \geq 1,25 \cdot 10^{-4} \\ &d \geq \sqrt{\frac{4 \cdot 1,25 \cdot 10^{-4}}{\pi}} \\ &d \geq 0,0126 \\ &d=0,013 \ [m]\\ \end{aligned} Pole przekroju na zwymiarowanej średnicy: \begin{aligned} &A=\frac{\pi \cdot 0,013^{2}}{4}=1,327 \cdot 10^{-4} \end{aligned} Naprężenia na przedziałach charakterystycznych: \begin{aligned} \sigma_{1} &=\frac{N_{1}}{A}=-\frac{10 \cdot 10^{3}}{1,327 \cdot 10^{-4}}=-75,36 \mathrm{MPa} \\ \sigma_{2} &=\frac{N_{2}}{2 A}=-\frac{10 \cdot 10^{3}}{2 \cdot 1,327 \cdot 10^{-4}}=-37,68 \mathrm{MPa} \\ \sigma_{3} &=\frac{N_{3}}{2 A}=\frac{10 \cdot 10^{3}}{2 \cdot 1,327 \cdot 10^{-4}}=37,68 \mathrm{MPa} \end{aligned} Wydłużenia \begin{aligned} &\Delta l=\frac{N \cdot l}{E \cdot A} \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot A}=\frac{-10 \cdot 10^{3} \cdot 2 \cdot 1}{2,1 \cdot 10^{11} \cdot 1,327 \cdot 10^{-4}}=-7,18 \cdot 10^{-4}[\mathrm{~m}]=-7,18 \cdot 10^{-4}[\mathrm{~mm}]=-0,718[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot 2 A}=\frac{-10 \cdot 10^{3} \cdot 1 \cdot 1}{2,1 \cdot 10^{11} \cdot 2 \cdot 1,327 \cdot 10^{-4}}=-1,79 \cdot 10^{-4}[\mathrm{~m}]=-0,179[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot 2 A}=\frac{10 \cdot 10^{3} \cdot 2 \cdot 1}{2,1 \cdot 10^{11} \cdot 2 \cdot 1,327 \cdot 10^{-4}}=1,79 \cdot 10^{-4}[\mathrm{~m}]=0,179[\mathrm{~mm}] \end{aligned} Podsumowanie: \begin{aligned} &N_{1}=10 k N \\ &N_{2}=-10 k N \\ &N_{3}=10 k N \\ &\sigma_{1}=-75,36 \mathrm{MPa} \\ &\sigma_{2}=-37,68 \mathrm{MPa} \\ &\sigma_{3}=37,68 \mathrm{MPa} \\ &\Delta l_{3}=0,179 \mathrm{~mm} \\ &\Delta l_{2}=-0,179 \mathrm{~mm} \\ &\Delta l_{1}=-0,718 \mathrm{~mm} \\ \end{aligned} Przemieszczenia \begin{aligned} &u_{I I I}=\Delta l_{3}=0,179 \mathrm{~mm} \\ &u_{I I}=\Delta l_{3}+\Delta l_{2}=0,179-0,179=0 \mathrm{~mm} \\ &u_{I}=\Delta l_{3}+\Delta l_{2}+\Delta l_{1}=-0,718 \mathrm{~mm} \end{aligned} Wykresy

Przykład 2

Treść

Dwustopniowy pręt został trwale utwierdzony końcem D i obciążony siłami P oraz 2P jak na rysunku.
Obliczyć jaka musi być wartość siły F, aby \(\Delta_l=0\)
Dane: \( d_1=20 cm, d_2=15 cm, E=2,1\cdot10^5 MPa, P=15 kN \)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Siły normalne na przedziałach charakterystycznych \begin{aligned} &N_{AB}=F\\ &N_{BC}=F-P\\ &N_{CD}=F-P+2P=F+P\\ \end{aligned} Wyrażam jedno pole przekroju za pomocą drugiego, żeby uprościć sobie dalsze obliczenia \begin{aligned} &\frac{A_{AB}}{A_{BC}}=\frac{\frac{\pi\cdot d_2^2}{4}}{\frac{\pi\cdot d_1^2}{4}}=\frac{d_2^2}{d_1^2}=\frac{9}{16}=0,5625\\ &A_{AB}=0,5625\cdot A_{BC}\\ \end{aligned} Rozwiązuje warunek z treści zadania - całkowite wydłużenie ma być równe zero \begin{aligned} &\Delta_{l_C}=\Delta_{l_{AB}}+\Delta_{l_{BC}}+\Delta_{l_{CD}}\\ &\Delta_l=\frac{N\cdot l}{E\cdot A}\\ \end{aligned} \begin{aligned}\\ &\frac{F\cdot 4}{E\cdot 0,5625\cdot A_{BC}} + \frac{(F-P)\cdot 3}{E\cdot A_{BC}} + \frac{(F+P)\cdot 1}{E\cdot A_{BC}}=0 \ \ \ |\cdot EA_{BC}\\ &\frac{4}{0,5625}F + 3F - 3P + F + P=0\\ &11,11F=2P\\ &F=0,18\cdot 15\cdot 10^{3}\\ &F=2,7 \ kN\\ \end{aligned} Sprawdzenie \begin{aligned} &\frac{2,6\cdot 10^{3}\cdot 4}{2,1\cdot 10^{11}\cdot\frac{\pi\cdot 0,15^{2}}{4}} + \frac{-12,3\cdot 10^{3}\cdot 3}{2,1\cdot 10^{11}\cdot\frac{\pi\cdot 0,2^{2}}{4}}+\frac{17,7\cdot 10^{3}\cdot 1}{2,1\cdot 10^{11}\cdot\frac{\pi\cdot 0,2^{2}}{4}}=6,17\cdot 10^{-9} \approx 0\\ \end{aligned}

Przykład 3

Treść

Oblicz średnicę wewnętrzną otworu, który można wywiercić osiowo na głębokości 3 metrów.
Dane: \(D=20 cm, E=85 GPa, P=15 kN, u_{max}=0,15 mm\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Warunek z treści zadania jest na maksymalne przemieszczenie "u". Wystąpi ono w jednym z punktów charakterystycznych A lub B \begin{aligned} &u_{B}=\Delta l_{BC}\\ &u_{A}=\Delta l_{BC}+\Delta l_{AB}\\ \end{aligned} Siły normalne na przedziałach charakterystycznych \begin{aligned} &N_{AB}=3P\\ &N_{BC}=3P-P=2P\\ \end{aligned} Siły normalne na obu przedziałach są dodatnie, a więc cały pręt jest rozciągany, wobec tego maksymalne przemieszczenie będzie na jego końcu (punkt A) \begin{aligned} &u_{max}=0,15 \ mm=0,15\cdot 10^{-3} \ m\\ &u_{max}=u_{A}=\Delta l_{BC}+\Delta l_{AB}\\ \end{aligned} Pola przekrojów poprzecznych na przedziale AB i BC \begin{aligned} &A_{AB}=\frac{\pi D^{2}}{4}\\ &A_{BC}=\frac{\pi D^{2}}{4} - \frac{\pi d^{2}}{4} = \frac{\pi(D^{2}-d^{2})}{4}\\ \end{aligned} Wzór na wydłużenie części pręta \begin{aligned} &\Delta l = \frac{N\cdot l}{E\cdot A}\\ \end{aligned} Ostatecznie zapisuję i rozwiązuję warunek z treści zadania \begin{aligned} &\frac{3P\cdot 2}{E\cdot\frac{\pi D^{2}}{4}} + \frac{2P\cdot 3}{E\cdot\frac{\pi(D^{2}-d^{2})}{4}} \le 0,15\cdot 10^{-3} \ \ \ \ |\cdot E\pi\\ &\frac{24P}{D^{2}}\cdot (D^{2}-d^{2}) + \frac{24P}{D^{2}-d^{2}}\cdot (D^{2}-d^{2}) \le 0,15\cdot 10^{-3}\cdot\pi\cdot E\cdot (D^{2}-d^{2})\\ &\frac{24P}{D^{2}}\cdot D^{2} - \frac{24P}{D^{2}}\cdot d^{2} + 24P \le 0,15\cdot 10^{-3}\cdot\pi\cdot E\cdot D^{2} - 0,15\cdot 10^{-3}\cdot\pi\cdot E\cdot d^{2}\\ &48\cdot 15\cdot 10^{3} - 9\cdot 10^{6}\cdot d^{2}\le 1,6\cdot 10^{6} - 40,06\cdot 10^{6}\cdot d^{2}\\ &48\cdot 15\cdot 10^{3} - 1,6\cdot 10^{6} \le (-40,06\cdot 10^{6} + 9\cdot 10^{6})\cdot d^{2}\\ \\ &d^{2}\ge \frac{48\cdot 15\cdot 10^{3} - 1,6\cdot 10^{6}}{-40,06\cdot 10^{6} + 9\cdot 10^{6}}\\ \\ &d\ge \sqrt\frac{48\cdot 15\cdot 10^{3} - 1,6\cdot 10^{6}}{-40,06\cdot 10^{6} + 9\cdot 10^{6}}\\ &d\ge 0,168 \ m\\ &d\ge 16,8 \ cm\\ \end{aligned}

Przykład 4

Treść

Oblicz średnicę pręta d oraz wydłużenie pręta\(\Delta_l\).
Dane: \(a=1 m, P=15 kN, q=8 \frac{kN}{m}, M=6 kNm, k_r=80 MPa, k_c=120 MPa, E=2\cdot10^5 MPa\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć
Siła w pręcie \begin{aligned} &\sum{M_A}=0\\ &-Pa+2qa\cdot 3a-M-S(2a\cdot sin60+2a\cdot cos60)=0\\ &S=\frac{-Pa+2qa\cdot 3a-M}{(2a\cdot sin60+2a\cdot cos60)}\\ &S=\frac{-15\cdot 1 + 2\cdot 8\cdot 3 - 6}{2\cdot\frac{\sqrt 3}{2}+2\cdot\frac{1}{2}}=9,88 \ kN\\ &S=9,88 kN\\ \end{aligned} Średnica z warunku wytrzymałościowego \begin{aligned} &\sigma=|\frac{N}{A}|\le k_{r},k_{c}\\ &A=\frac{\pi d^{2}}{4}\\ &N=9,88\cdot 10^{3} \ N\\ &k_{r}=80 \ MPa\\ &\frac{9,88\cdot 10^{3}}{\frac{\pi d^{2}}{4}} \le 80\cdot 10^{6}\\ &\frac{9,88\cdot 10^{3}\cdot 4}{80\cdot 10^{6}\cdot\pi}\le d^{2}\\ &d\ge 0,0125 \ m\\ &d\ge 1,25 \ cm\\ \end{aligned} Wydłużenie pręta \begin{aligned}\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &A=\frac{\pi d^{2}}{4}\\ &d \ge 1,25 \ cm\\ &d=1,3 \ cm\\ &A=\frac{\pi(1,3\cdot 10^{-2})^{2}}{4}=1,33\cdot 10^{-4} \ m^{2}\\ &E=2\cdot 10^{5}\cdot 10^{6} Pa\\ &N=9,88\cdot 10^3 \ N\\ &\Delta l=\frac{9,88\cdot 10^{3}\cdot 1}{2\cdot 10^{11}\cdot 1,33\cdot 10^{-4}}=3,8\cdot 10^{-4} \ m=0,38 \ mm\\ \end{aligned}

Przykład 5

Treść

Oblicz na jakiej odległości x należy przyłożyć siłę skupioną P, aby wydłużenia prętów spowodowały równoległe przemieszczenia belki AB w dół. Wszystkie pręty mają jednakowy przekrój kołowy.
Dane: \(l=1 m, P=10 kN\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć
Obliczenie reakcji z równań równowagi statycznej \begin{aligned} &\sum{M_{A}}=0\\ &P\cdot x - N_{3}\cdot 2l=0\\ &N_{3}=\frac{1}{2}Px\\ \\ &\sum{X}=0\\ &-N_{1}\cdot\sin\alpha + N_{2}\cdot\sin\alpha=0\\ &N_{1}=N_{2}\\ \\ &\sum{Y}=0\\ &N_{1}\cdot \cos\alpha + N_{2}\cos\alpha - P + N_{3}=0\\ &N_{1}\cdot\cos\alpha + N_{1}\cdot\cos\alpha=P- \frac{1}{2}Px\\ &N_{1}=\frac{P(1-\frac{1}{2}x)}{2\cdot\cos\alpha}\\ &\cos60^{o}=P(1-\frac{1}{2}x)\\ &N_{1}=P(1-\frac{1}{2}x)\\ &N_{2}=P(1-\frac{1}{2}x)\\ \end{aligned} Warunek geometryczny z treści zadania

Aby belka przemieściła się równolegle w dół - przemieszczenie punktu A i B muszą być takie same \begin{aligned} &f_{A}=f_{B}\\ &f_{B}=\Delta l_{3}\\ &\frac{\Delta l_{2}}{f_{A}}=\cos60^{o}=\frac{1}{2}\\ &f_{A}=2\cdot\Delta l_{2}\\ &2\cdot\Delta l_{2}=\Delta l_{3}\\ \end{aligned} Obliczamy wydłużenia prętów \begin{aligned} &\Delta l=\frac{Nl}{EA}\\ &\Delta l_{2}=\frac{P(1-\frac{1}{2}x)\cdot 1}{EA}\\ &\Delta l_{3}=\frac{\frac{1}{2}Px\cdot 1}{EA}\\ \end{aligned} Podstawiamy do warunku geometrycznego i obliczamy położenie siły "x" \begin{aligned} &2\cdot\frac{P(1-\frac{1}{2}x)\cdot 1}{EA}=\frac{\frac{1}{2}Px\cdot 1}{EA} \ \ \ \ \ |\cdot EA\\ &2\cdot P(1-\frac{1}{2}x)=\frac{1}{2}Px \ \ \ \ \ \ |:P\\ &x=\frac{4}{3} m\\ \end{aligned}

Przykład 6

Treść

Na wsporniku ABC składającym się z miedzianej podpory AB oraz stalowego cięgna AC zawieszono ciężar G=50kN. Określić średnicę D cięgna oraz wymiar a przekroju kwadratowego miedzianej podpory AB, przyjmując dane naprężenia dopuszczalne dla miedzi i stali. Określić przemieszczenie poziome i pionowe punktu A.
Dane: \( k_c (m)=40 MPa, k_r (st)=160 MPa, E_s=2,1\cdot 10^5 MPa, E_m=1,15\cdot 10^5 MPa, AB=1,2 m\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Rzutowanie siły w pręcie AC na składową poziomą i pionową.

Równania równowagi statycznej dla węzła A. \begin{aligned} &\sum{Y}=0\\ &N_{AC}\cdot\sin30^{o}=0\\ &N_{AC}=2G\\ &\sum{X}=0\\ &-N_{AB}-N_{AC}\cdot\cos30^{o}=0\\ &N_{AB}=-2G\cdot\frac{\sqrt3}{2}\\ &N_{AB}=-G\sqrt3\\ \end{aligned} Warunek wytrzymałościowy
Pręt AB
\begin{aligned}&\sigma=|\frac{N}{A}|\le k\\ \\ &\sigma_{AB}=\frac{G\sqrt2}{a^{2}}\le 40 \ MPa\\ &\frac{50\cdot 10^{3}\cdot \sqrt3}{40\cdot 10^{6}}\le a^{2}\\ &a\ge \sqrt\frac{50\cdot 10^{3}\cdot \sqrt3}{40\cdot 10^{6}}\\ &a\ge 0,0465 \ m\\ &a=0,047 \ m=4,7 \ cm\\ \end{aligned}
Pręt AC
\begin{aligned} &\sigma_{AC}=\frac{2G}{\frac{\pi d^{2}}{4}}\le 160 \ MPa\\ &\frac{2\cdot 50\cdot 10^{3}\cdot 4}{160\cdot 10^{6}\cdot\pi}\le d^{2}\\ &d\ge \sqrt\frac{2\cdot 50\cdot 10^{3}\cdot 4}{160\cdot 10^{6}\cdot\pi}\\ &d\ge 0,0282 \ m\\ &d=0,03 \ m=3 \ cm\\ \end{aligned} Narysowanie planu przemieszczeń w celu obliczenia przemieszczenia poziomego i pionowego punktu A.
Odkładamy wydłużenia i skrócenia prętów (w ich osiach).

Obliczamy wydłużenie pręta AC (dodatnia siła w pręcie) oraz skrócenie pręta AB (siła ujemna - pręt ściskany). \begin{aligned} \Delta l &= \frac{Nl}{EA} \\ \Delta l_{AB} &= \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{E_{m} \cdot a^{2}} = \frac{-50 \cdot \sqrt{3} \cdot 10^{3} \cdot 1.2}{1.15 \cdot 10^{11} \cdot 0.047^{2}} = -4.09 \times 10^{-4} \ m = -0.409 \ mm \end{aligned} Obliczam długość pręta AC oraz jego wydłużenie. \begin{aligned} &\frac{1,2}{|AC|}=\cos30^{o} & \\ & |AC|=\frac{1,2}{\cos30^{o}}=1,386\\ &\Delta l_{AC}=\frac{50\cdot 2\cdot 10^{3}\cdot |AC|}{E_{s}\cdot\frac{\pi d^{2}}{4}}=\frac{50\cdot 2\cdot 10^{3}\cdot 1,386\cdot 4}{2,1\cdot 10^{11}\cdot\pi\cdot 0,03^{2}}=9,337\cdot 10^{-4} \ m=0,934 \ mm\\ \end{aligned} Zaznaczam dopuszczalną linię przemieszczeń wydłużonych/skróconych prętów i znajduję ich przecięcie - w to miejsce ostatecznie przemieści się punkt A.

Zauważam zielony trójkąt, opisuję dwa z jego boków jako a,b oraz zauważam że jest on podobny do małego trójkąta a', b', \( \Delta l_{AB} \).

Obliczam bok a. \begin{aligned} &a=a' + |\Delta l_{AC}|\\ &|\Delta l_{AC}|=0,934 \ mm\\ &\frac{|\Delta l_{AB}|}{a'}=\cos30^{o}\\ &a'=\frac{0,409}{\frac{\sqrt3}{2}}=0,47 \ mm\\ &a=0,47 + 0,934 = 1,404 \ mm \end{aligned} Obliczam bok b. \begin{aligned} &b=b' + \Delta_{y}\\ &\frac{b'}{a'}=sin30^{o}\\ &b'=0,47\cdot 0,5 = 0,235 \ mm\\ &\frac{a}{b}=\sin30^{o}\\ &b=\frac{a}{sin30^{o}}=\frac{1,404}{0,5}\\ &b=2,808 \ mm\\ \end{aligned} Obliczam przemieszczenie pionowe i poziome punktu A. \begin{aligned} &\Delta_{y}=b-b'\\ &\Delta_{y}=2,808 - 0,235 = 2,573 \ mm\\ &\Delta_{x}=\Delta l_{AB} = 1,438 \ mm\\ \end{aligned}

Przykład 7

Treść

Dwustopniowy pręt został trwale utwierdzony końcem A, końcem D i obciążony siłami jak na rysunku. Obliczyć reakcję w utwierdzeniach, wskazać w której części pręta powstają największe naprężenia.
Dane: \( A_1=2\cdot A_2, 2\cdot E_1=E_2 \)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Obliczenie reakcji
Warunek statyki
\begin{aligned} &\sum X=0 \\ &R_{A}+15-20-R_{B}=0 \\ \end{aligned}
Warunek geometryczny
\begin{aligned} &\Delta l_{c}=0 \\ &\Delta l_{A B}+\Delta l_{B C}+\Delta l_{C D}=0 \\ &\Delta l=\frac{N \cdot l}{E \cdot A} \end{aligned} Rozpisanie sił normalnych na przedziałach charakterystycznych \begin{aligned} &N_{AB}=R_{A}\\ &N_{BC}=R_{A}+15\\ &N_{CD}=R_{A} + 15 - 20=R_{A} - 5\\ \end{aligned} Rozwiązanie warunku geometrycznego \begin{aligned} &\frac{R_{A}\cdot 1}{E_{1}\cdot A_{1}}+\frac{(R_{A}+15)\cdot 3}{E_{1}\cdot A_{1}}+\frac{(R_{A}-5)\cdot 3}{E_{2}\cdot A_{2}}=0\\ &\frac{R_{A}}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}+45}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}-15}{2E_{1}\cdot A_{2}}=0 & |\cdot E_{1}\cdot A_{2}\\ &\frac{1}{2}R_{A}+\frac{3}{2}R_{A}+22,5+\frac{3}{2}R_{A}-7,5=0\\ &3,5R_{A}=-15\\ &R_{A}=-4,286 \ kN\\ &R_{A}+15 - 20 - R_{B}=0\\ &R_{B}=-9,286 \ kN\\ \end{aligned} Po obliczeniu reakcji RA ostatecznie siły na przedziałach mają wartości: \begin{aligned} &N_{AB}=R_{A}=-4,286 \ kN\\ &N_{BC}=R_{A}+15=10,714 \ kN\\ &N_{CD}=R_{A}+15-20=R_{A}-5=-9,286 \ kN \\ \end{aligned} Rozpisanie naprężeń normalnych na przedziałach charakterystycznych \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{AB}=\frac{-4,286}{A_{1}}=\frac{-4,286}{2A_{2}}=-2,143\cdot\frac{1}{A_{2}}\\ &\sigma_{BC}=\frac{10,714}{A_{1}}=\frac{10,714}{2A_{2}}=5,357\cdot\frac{1}{A_{2}}\\ &\sigma_{CD}=\frac{9,286}{A_{2}}=9,286\cdot\frac{1}{A_{2}}\\ \end{aligned} Wykresy

Przykład 8

Treść

Belka zamocowana przegubowo i zaczepiona dwoma prętami obciążona jest obciążeniem ciągłym. Z warunku wytrzymałościowego policz średnicę prętów.
Dane: \( A_1=A_2, E_1=2\cdot E_2, k_r=60\ MPa, k_c=90\ MPa \)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Zaznaczam reakcje podporowe oraz siły w prętach kratowych

Zapisuję jedno równanie równowagi statycznej - takie w którym niewiadome będą siły w prętach \( N_1, N_2 \) \begin{aligned} &\sum{M_{A}}=0\\ &N_{1}\cdot 2 - N_{2}\cdot \sin\alpha\cdot 6 + 8\cdot 4\cdot 4=0\\ &N_{1}=3N_{2}\cdot\sin\alpha - 64\\ &\sin\alpha=\frac{3}{5} & \cos\alpha=\frac{4}{5}\\ &N_{1}=1,8N_{2}-64\\ \end{aligned} Rozrysowuję plan przemieszczeń, aby rozpisać warunek geometryczny (zależność pomiędzy przemieszczeniami z podobieństwa trójkątów)
Pręty mogą wydłużać się w swoich osiach, natomiast dopuszczalna linia przemieszczeń wydłużonego/skróconego końca pręta jest na kierunku prostopadłym do osi pręta.
Dodatkowo pamiętam, że każdy punkt nieodkształcalnej poziomej belki może się znaleźć na kierunku prostopadłym do tej osi.

Warunek geometryczny \begin{aligned} &\frac{f_{B}}{2}=\frac{f_{A}}{6}\\ &\frac{\Delta l_{2}}{f_{A}}=\sin\alpha \ \ \ \Rightarrow \ \ \ f_{A}=\frac{\Delta l_{2}}{\sin\alpha}\\ &f_{B}=\Delta l_{1}\\ &\frac{\Delta l_{1}}{2}=\frac{\frac{\Delta l_{2}}{\sin\alpha}}{6}\\ &6\sin\alpha\cdot\Delta l_{1}=2\cdot\Delta l_{2}\\ &6\cdot 0,6\cdot\frac{-N_{1}\cdot 3}{E_{1}\cdot A_{1}}=2\cdot\frac{N_{2}\cdot 5}{E_{2}\cdot A_{2}}\\ &\frac{-10,8N_{1}}{2E_{2}\cdot A_{2}}=\frac{10N_{2}}{E_{2}\cdot A_{2}} \ \ \ \ \ \ \ \ |\cdot E_{2}A_{2}\\ &-5,4N_{1}=10N_{2}\\ &N_{1}=-1,85N_{2} \end{aligned} Otrzymujemy drugą zależność pomiędzy \(N_1 \) oraz \(N_2 \), wracamy do pierwszej zależności i obliczamy siły w prętach
\begin{aligned} &N_{1}=1,85N_{2}-64\\ &-1,85N_{2}=1,8N_{2}-64\\ \\ &N_{2}=17,53 \ kN\\ &N_{1}=-32,43 \ kN\\ \end{aligned} Warunek wytrzymałościowy \begin{aligned} &\sigma=\frac{|N|}{A}\le k\\ \end{aligned} \begin{array}{ll} \sigma_{1}=\frac{32,43 \cdot 10^{3}}{A} \leq 90 \cdot 10^{6} & \Rightarrow A \geq 3,6 \cdot 10^{-4} \mathrm{~m}^{2} \\ \sigma_{2}=\frac{17,53 \cdot 10^{3}}{A} \leq 60 \cdot 10^{6} & \Rightarrow A \geq 2,92 \cdot 10^{-4} \mathrm{~m}^{2} \\ \end{array} Decyduje pierwszy warunek, przyjmuję: \begin{array}{ll}A=3,65 \cdot 10^{-4} \mathrm{~m}^{2} & \Rightarrow d=0,0215 \mathrm{~m}=2,15 \mathrm{~cm} \\ A=\frac{\pi d^{2}}{4} \end{array}

Przykład 9

Treść

Drewniana belka podwieszona jest na trzech prętach - pierwszy i trzeci wykonane są ze stali, drugi jest miedziany, o długościach \( l_1=3m, l_2=2m, l_3=4m \)
Oblicz jakie naprężenia powstają w prętach.
Dane: \( k_{r_st}=120 MPa, k_{r_m}=30 MPa, A_1=A_2=2\cdot A_3, E_2=105 GPa, E_1=E_3=210 GPa\)

Kurs wideo

Rozwiązanie
Rozwiązanie - Kliknij, aby rozwinąć Suma rzutów sił na oś x nic nam nie daje, więc mamy dwa efektywne równania równowagi statycznej. Niewiadome są siły w trzech prętach, a więc zadanie jest jednokrotnie statycznie niewyznaczalne, do jego rozwiązanie musimy wykorzystać dodatkowy warunek - geometryczny (z planu przemieszczeń).
Równania równowagi:
\begin{aligned} &\sum{M_{C}}=0\\ &N_{1}\cdot 4 - 75\cdot 2 - N_{3}\cdot 4 = 0\\ &N_{1}=\frac{150 + 4\cdot N_{3}}{4}\\ &N_{1}=37,5 + N_{3}\\ &\sum{Y}=0\\ &N_{1} - 75 + N_{2} + N_{3} =0\\ &37,5 + N_{3} - 75 + N_{3}=-N_{2}\\ &N_{2}=37,5 - 2N_{3} \end{aligned}
Warunek geometryczny \begin{aligned} &\frac{\Delta l_{3}-\Delta l_{1}}{8}=\frac{\Delta l_{2}-\Delta l_{1}}{4}\\ \end{aligned} Przekształcam i rozwiązuję warunek geometryczny \begin{aligned} &\Delta l_{3}-\Delta l_{1}=2(\Delta l_{2}-\Delta l_{1})\\ &\Delta l_{3}+\Delta l_{1}-2\cdot \Delta l_{2}=0\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &\frac{N_{3}\cdot 4}{E_{3}\cdot A_{3}}+\frac{N_{1}\cdot 3}{E_{1}\cdot A_{1}}-2\cdot \frac{N_{2}\cdot 2}{E_{2}\cdot A_{2}}=0 \end{aligned} Z treści zadania: \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &\frac{E_{2}}{E_{1}}=\frac{105 \ GPa}{210 \ GPa}=\frac{1}{2} & \Rightarrow 2E_{2}=E_{1}\\ &E_{1}=E_{3}\\ \end{aligned} Podstawiam te zależności do wcześniejszego równania \begin{aligned} &\frac{N_{3}\cdot 4}{2E_{2}\cdot A_{3}}+\frac{(37,5 + N_{3})\cdot 3}{2E_{2}\cdot 2A_{3}} - 2\cdot\frac{(37,5 - 2N_{3})\cdot 2}{E_{2}\cdot 2A_{3}}=0 & |\cdot E_{2}A_{3}\\ &2N_{3} + \frac{3}{4}(37,5 + N_{3}) - 2(37,5 - 2M_{3})=0\\ &2N_{3} + 28,125 + 0,75N_{3} - 75 + 2N_{3}\\ &4,75N_{3}=46,875\\ &N_{3}=9,868 \ kN \end{aligned} Wracam do zależności z równań równowagi statycznej i obliczam siły w pozostałych prętach \begin{aligned} &N_{1}=37,5 + N_{3}=47,368 \ kN\\ &N_{2}=37,5 - 2N_{3}=17,764 \ kN\\ \end{aligned} Rozwiązuję warunek wytrzymałości dla wszystkich prętów \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{1}=\frac{47,368\cdot 10^{3}}{A_{1}}\le 120\cdot 10^{6} & \Rightarrow & A_{1}\ge 3,95\cdot 10^{-4} \ m^{2}\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{A_{2}}\le 30\cdot 10^{6} & \Rightarrow & A_{2}\ge 5,92\cdot 10^{-4} \ m^{2}\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{A_{3}}\le 120\cdot 10^{6} & \Rightarrow & A_{3}\ge 8,22\cdot 10^{-5} \ m^{2}\\ \end{aligned} Przyjmuję ostatecznie pole przekroju dla prętów pamiętając o zależności z treści zadania \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &A_{1}=A_{2}=6\cdot 10^{-4}\\ &A_{3}=\frac{1}{2}\cdot 6\cdot 10^{-4}=3\cdot 10^{-4}\\ \end{aligned} Obliczam naprężenia w prętach dla przyjętego pola przekroju poprzecznego \begin{aligned} &\sigma_{1}=\frac{47,368\cdot 10^{3}}{6\cdot 10^{-4}}=78,95 \ MPa\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{6\cdot 10^{-4}}=29,60 \ MPa\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{3\cdot 10^{-4}}=32,89 \ MPa\\ \end{aligned}

↓ odnośnik do bazy zadań z rozwiązaniami oraz do kursów wideo ↓

Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz 4 zadania z tego działu!
(rozciąganie statycznie wyznaczalne)
pojedyncze pręty Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz 17 zadań z tego działu!
(rozciąganie statycznie wyznaczalne)
układy prętów Zobacz wideo-kurs z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz 11 zadań z tego działu!
(rozciąganie statycznie niewyznaczalne) Zobacz zadania z użyciem podstawowych definicji